
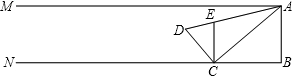
如图,射线BN、AM都垂直于线段AB,E为AM上一动点, ⊥
⊥ 于F,交BN于C,
于F,交BN于C, ⊥
⊥ 于
于 ,连接BD.
,连接BD.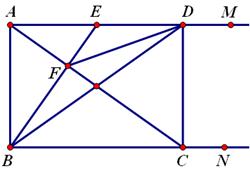
⑴求证: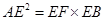 ;
;
⑵当 为
为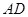 的中点时,求证:
的中点时,求证:  ;
;
⑶设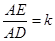 ,请探究出使
,请探究出使 为
为
等腰三角形的实数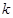 的值.
的值.
科目:初中数学 来源: 题型:
| AE | AD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,射线AM∥BN,∠A=∠B=90°,点D、C分别在AM、BN上运动(点D不与A重合、点C不与B重合),E是AB边上的动点(点E不与A、B重合),在运动过程中始终保持DE⊥EC且AD+DE=AB=a.
如图,射线AM∥BN,∠A=∠B=90°,点D、C分别在AM、BN上运动(点D不与A重合、点C不与B重合),E是AB边上的动点(点E不与A、B重合),在运动过程中始终保持DE⊥EC且AD+DE=AB=a.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏盐城九年级中考模拟考试数学试卷(解析版) 题型:解答题
如图,射线BN、AM都垂直于线段AB,E为AM上一动点, ⊥
⊥ 于F,交BN于C,
于F,交BN于C, ⊥
⊥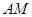 于
于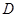 ,连接BD.
,连接BD.
⑴求证:  ;
;
⑵当 为
为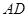 的中点时,求证:
的中点时,求证:
 ;
;
⑶设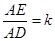 ,请探究出使
,请探究出使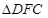 为
为
等腰三角形的实数 的值.
的值.
【解析】(1)中利用 ⊥
⊥
得到直角三角形AEF相似于三角形ABE,然后得到结论。
(2)中,
由⑴有 ,因为
,因为 为
为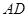 的中点,所以
的中点,所以
则可以得到

从而的得到角相等
(3)中,设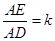 ,当使
,当使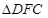 为
为
等腰三角形时,需要考查谁是腰,分类讨论得到
①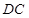 为腰,且
为腰,且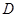 为顶角顶点;
为顶角顶点;
②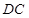 为腰,且
为腰,且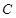 为顶角顶点;
为顶角顶点;
③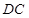 为底.
为底.
①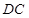 为腰,且
为腰,且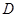 为顶角顶点;
为顶角顶点;
解得答案为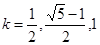
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com