【题目】如图，正方形ABCD中．点E，F分别在BC，CD上，△AEF是等边三角形．连接AC交EF于点G．过点G作GH⊥CE于点H．若
，则
=（ ）
A. 6 B. 4 C. 3 D. 2
【答案】A
【解析】解：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=∠BCD=∠D=∠BAD=90°．
∵△AEF等边三角形，∴AE=EF=AF，∠EAF=60°，∴∠BAE+∠DAF=30°．
在Rt△ABE和Rt△ADF中，∵AE=AF，AB=AD，∴Rt△ABE≌Rt△ADF（HL），∴BE=DF，∵BC=CD，∴BC﹣BE=CD﹣DF，即CE=CF，∴△CEF是等腰直角三角形，∵AE=AF，∴AC垂直平分EF，∴EG=GF，∵GH⊥CE，∴GH∥CF，∴△EGH∽△EFC，∵S△EGH=3，∴S△EFC=12，∴CF=
，EF=
，∴AF=
，设AD=x，则DF=x﹣
，∵AF2=AD2+DF2，∴（
）2=x2+（x﹣
）2，∴x=
，∴AD=
，DF=
，∴S△ADF=
ADDF=6．故选A．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．
（1）在给定方格纸中画出平移后的△A′B′C′；
（2）画出AB边上的中线CD和BC边上的高线AE；
（3）线段AA′与线段BB′的关系是： ；
（4）求四边形ACBB′的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明骑单车上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的某书店，买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图．
根据图中提供的信息回答下列问题：
（1）小明家到学校的路程是________米
（2）小明在书店停留了___________分钟．
（3）本次上学途中，小明一共行驶了________ 米，一共用了______ 分钟．
（4）在整个上学的途中_________（哪个时间段）小明骑车速度最快，最快的速度是___________米/分．
查看答案和解析>>
科目：初中数学 来源： 题型：
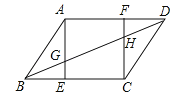
【题目】如图，在平行四边形ABCD中，AE⊥BC，CF⊥AD，垂足分别为E，F，AE，CF分别与BD交于点G和H，且AB=
．
（1）若tan∠ABE =2，求CF的长；
（2）求证：BG=DH．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，坐标原点O是菱形ABCD的对称中心．边AB与x轴平行，点B（1，-2），反比例函数
（k≠0）的图象经过A，C两点．
（1）求点C的坐标及反比例函数的解析式．
（2）直线BC与反比例函数图象的另一交点为E，求以O，C，E为顶点的三角形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场计划购进A、B两种商品，若购进A种商品2件和B种商品1件需45元；若购进A种商品3件和B种商品2件需70元．
（1）A、B两种商品每件的进价分别是多少元？
（2）若购进A、B两种商品共100件，总费用不超过1000元，最多能购进A种商品多少件？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
