
【题目】如图,四边形ABCD中,∠B=90°, AB//CD,M为BC边上的一点,AM平分∠BAD,DM平分∠ADC,
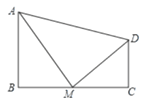
求证:(1) AM⊥DM;
(2) M为BC的中点.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)根据平行线的性质得到∠BAD+∠ADC=180°,根据角平分线的定义得到∠MAD+∠ADM=90°,求出∠AMD=90°,根据垂直的定义得到答案;
(2)作MN⊥AD,根据角平分线的性质得到BM=MN,MN=CM,等量代换可得结论.
证明:(1)∵AB∥CD,
∴∠BAD+∠ADC=180°,
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180°,
∴∠MAD+∠ADM=90°,
∴∠AMD=90°,即AM⊥DM;
(2)作MN⊥AD交AD于N,
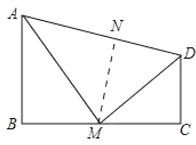
∵∠B=90°,AB∥CD,
∴BM⊥AB,CM⊥CD,
∵AM平分∠BAD,DM平分∠ADC,
∴BM=MN,MN=CM,
∴BM=CM,即M为BC的中点.


科目:初中数学 来源: 题型:
【题目】下列命题:①两条直线相交,一个角的两邻补角相等,则这两条直线垂直;②同位角相等;③点(5,6)与点(6,5)表示同一点;④若两个同旁内角互补,则它们的角平分线互相垂直;⑤点(![]() ,5)在第二象限.其中假命题的个数为( )
,5)在第二象限.其中假命题的个数为( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( )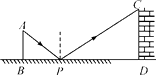
A.6米
B.8米
C.18米
D.24米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则S△DAC:S△ABC=_____.
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则S△DAC:S△ABC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
已知,在Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕点D旋转,它的两边分别交AC,CB(或它们的延长线)于点E,F.

(1)(问题发现)
如图1,当∠EDF绕点D旋转到DE⊥AC于点E时(如图1),
①证明:△ADE≌△BDF;
②猜想:S△DEF+S△CEF= S△ABC.
(2)(类比探究)
如图2,当∠EDF绕点D旋转到DE与AC不垂直时,且点E在线段AC上,试判断S△DEF+S△CEF与S△ABC的关系,并给予证明.
(3)(拓展延伸)
如图3,当点E在线段AC的延长线上时,此时问题(2)中的结论是否成立?若成立,请给予证明;若不成立,S△DEF,S△CEF,S△ABC又有怎样的关系?(写出你的猜想,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H
(1) 求证:HE=HG
(2) 如图2,当BE=AB时,过点A作AP⊥DE于点P连接BP,求![]() 的值
的值
(3) 在(2)的条件下,若AD=2,∠ADE=30°,则BP的长为______________


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com