练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

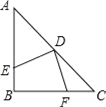
    【题目】如图，在△ABC中，∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°，求∠EDF的度数。

    【答案】∠EDF＝68°．

    【解析】

    由FD⊥BC，得∠FDC＝90°；因∠AFD是△CDF的外角，∠AFD＝158°，所以∠C＝∠AFD∠FDC＝158°90°＝68°．由∠B＝∠C，可得出∠B的度数．由DE⊥AB，得∠DEB＝90°，进而求得∠BDE的度数，则∠EDF的度数即可求得.

    ∵FD⊥BC，所以∠FDC＝90°，

    ∵∠AFD＝∠C+∠FDC，

    ∴∠C＝∠AFD﹣∠FDC＝158°﹣90°＝68°，

    ∴∠B＝∠C＝68°．

    ∵DE⊥AB，

    ∴∠DEB＝90°，

    ∴∠BDE＝90°﹣∠B＝22°．

    又∵∠BDE+∠EDF+∠FDC＝180°，

    ∴∠EDF＝180°﹣∠BDE﹣∠FDC＝180°﹣22°﹣90°＝68°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点P是∠AOB内任意一点，且∠AOB＝40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时,则∠MPN的度数为（ ）

    A. 140° B. 100° C. 50° D. 40°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和不完整的频数分布直方图，请根据图表信息回答下列问题：

    初中毕业生视力抽样调查频数分布表

    视力

    频数（人）

    频率

    4.0≤x＜4.3

    20

    0.1

    4.3≤x＜4.6

    40

    0.2

    4.6≤x＜4.9

    70

    0.35

    4.9≤x＜5.2

    a

    0.3

    5.2≤x＜5.5

    10

    b

    （1）本次调查的样本容量为　 　；

    （2）在频数分布表中，a=　 　，b=　 　，并将频数分布直方图补充完整；

    （3）若视力在4.6以上（含4.6）均属正常，根据上述信息估计全区初中毕业生中视力正常的学生有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC=2，∠B=∠C=40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E．

    （1）当∠BDA=115°时，∠EDC=______°，∠DEC=______°；点D从B向C运动时，∠BDA逐渐变______（填“大”或“小”）；

    （2）当DC等于多少时，△ABD≌△DCE，请说明理由；

    （3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数．若不可以，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰三角形ABC中，∠ABC=90°，D为AC边上中点，过D点作DE⊥DF，交AB于E，交BC于F，若S四边形BFDE=9，则AB的长为：

    A. 3 B. 6 C. 9 D. 18

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知中， ， ， ，D是AB边的中点，E是AC边上一点，联结DE，过点D作交BC边于点F，联结EF．

    （1）如图1，当时，求EF的长；

    （2）如图2，当点E在AC边上移动时， 的正切值是否会发生变化，如果变化请说出变化情况；如果保持不变，请求出的正切值；

    （3）如图3，联结CD交EF于点Q，当是等腰三角形时，请直接写出BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形ABCD中，AC为对角线，延长CD至点E使CE=CA，连接AE。F为AB上一点，且BF=DE，连接FC.

    （1）若DE=1，CF=2，求CD的长。

    （2）如图2，点G为线段AE的中点，连接BG交AC于H，若∠BHC+∠ABG=600，求证：AF+CE=AC.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，平面直角坐标系中，抛物线y=ax2﹣4ax+c与直线y=kx+1（k≠0）交于y轴上一点A和第一象限内一点B，该抛物线顶点H的纵坐标为5．

    （1）求抛物线的解析式；

    （2）连接AH、BH，抛物线的对称轴与直线y=kx+1（k≠0）交于点K，若S△AHB=，求k的值；

    （3）在（2）的条件下，点P是直线AB上方的抛物线上的一动点（如图2），连接PA．当∠PAB=45°时，

    ⅰ）求点P的坐标；

    ⅱ）已知点M在抛物线上，点N在x轴上，当四边形PBMN为平行四边形时，请求出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，AB=6，BC=8．

    （1）求对角线AC的长；

    （2）点E是线段CD上的一点，把△ADE沿着直线AE折叠．点D恰好落在线段AC上，与点F重合，求线段DE的长．

    查看答案和解析>>

    同步练习册答案