


| ½ā£ŗ£Ø1£©øł¾Ż×ų±źĻµæÉÖŖ“ĖŗÆŹż¶„µć×ų±źĪŖ£Ø5£¬6.25£©£¬ ”ąÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖ  £¬ £¬”ßĶ¼Ļó¹ż£Ø10£¬0£©µć£¬ ”ą  £¬ £¬½āµĆ 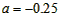 £¬ £¬”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖ 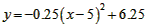 £» £» |
|
| £Ø2£©µ±×īæķ3m£¬×īøß3.5mµÄĮ½Į¾ĻįŹ½»õ³µ¾ÓÖŠ²¢ĮŠŠŠŹ»Ź±£¬x=2£¬ °Ńx=2“śČė½āĪöŹ½µĆ£ŗy=-0.25£Ø2-5£©2+6.25£¬y=4£¬ ”ß4-3.5=0.5£¬ ”ąĖķµĄÄÜČĆ×īæķ3m£¬×īøß3.5mµÄĮ½Į¾ĻįŹ½»õ³µ¾ÓÖŠ²¢ĮŠŠŠŹ»£» |
|
| £Ø3£©I£®¼ŁÉčAO=x£¬æɵĆAB=10-2x£¬ ”ąAD=-0.25£Øx-5£©2+6.25£¬ ”ą¾ŲŠĪABCDµÄÖܳ¤ĪŖl£ŗ l=2[-0.25£Øx-5£©2+6.25]+2£Ø10-2x£©=-0.5x2+x+20=-0.5£Øx-1£©2+20.5£¬ ”ąlµÄ×ī“óÖµĪŖ20.5£¬ II£®µ±ŅŌP”¢N”¢QĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬ ”ßPŌŚy=xµÄĶ¼ĻóÉĻ£¬ÉčP£Øm£¬m£©£¬ ¹żPµć×÷xÖįµÄ“¹Ļß½»Å×ĪļĻßÓŚµćQ£¬ ”ą”ĻPOA=”ĻOPA=45”ć£¬NµćµÄ×ų±źĪŖ£Ø5£¬5£©£¬ ”ąQµćµÄ×ų±źĪŖ£Øm£¬5£©£¬ °ŃQµćµÄ×ų±ź“śČė  £¬µĆ £¬µĆ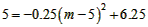 £¬ £¬½āµĆ 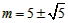 £¬ £¬”ąŹ¹ŅŌP”¢N”¢QĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬PµćµÄ×ų±źĪŖ£ŗ£Ø 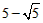 £¬ £¬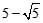 £©»ņ£Ø£¬ £©»ņ£Ø£¬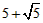 £©”£ £©”£ |
 |


 ½š°ęæĪĢĆæĪŹ±ŃµĮ·ĻµĮŠ“š°ø
½š°ęæĪĢĆæĪŹ±ŃµĮ·ĻµĮŠ“š°ø µ„ŌŖČ«ÄÜĮ·æ¼¾ķĻµĮŠ“š°ø
µ„ŌŖČ«ÄÜĮ·æ¼¾ķĻµĮŠ“š°ø ŠĀ»ĘøŌ±ų·ØĆܾķĻµĮŠ“š°ø
ŠĀ»ĘøŌ±ų·ØĆܾķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| æĪĢā | ²āĮæŠ£ÄŚĘģøĖøß¶Č | ||
| ÄæµÄ | ŌĖÓĆĖłŃ§ŹżŃ§ÖŖŹ¶¼°ŹżŃ§·½·Ø½ā¾öŹµ¼ŹĪŹĢā---²āĮæĘģøĖøß¶Č | ||
| ·½°ø | ·½°øŅ» | ·½°ø¶ž | ·½°øČż |
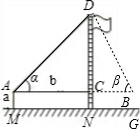
Ź¾ŅāĶ¼ |
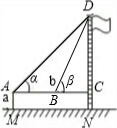 |
 |
|
| ²āĮ湤¾ß | ʤ³ß”¢²ā½ĒŅĒ | ʤ³ß”¢²ā½ĒŅĒ | |
| ²āĮæŹż¾Ż | AM=1.5m£¬AB=10m ”Ļ¦Į=30”ć£¬”Ļ¦Ā=60”ć |
AM=1.5m£¬AB=20m ”Ļ¦Į=30”ć£¬”Ļ¦Ā=60”ć |
|
| ¼ĘĖć¹ż³Ģ£Ø½į ¹ū±£ĮōøłŗÅ£© |
½ā£ŗ | ½ā£ŗ | |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| æĪĢā | ²āĮæŠ£ÄŚĘģøĖøß¶Č | ||
| ÄæµÄ | ŌĖÓĆĖłŃ§ŹżŃ§ÖŖŹ¶¼°ŹżŃ§·½·Ø½ā¾öŹµ¼ŹĪŹĢā----²āĮæĘģøĖøß¶Č | ||
| ·½°ø | ·½°øŅ» | ·½°ø¶ž | ·½°øČż |
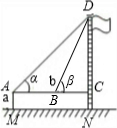
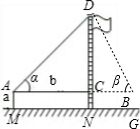
Ź¾ŅāĶ¼ |
 |
 |
|
| ²āĮ湤¾ß | ʤ³ß”¢²ā½ĒŅĒ | ʤ³ß”¢²ā½ĒŅĒ | |
| ²āĮæŹż¾Ż | AM=1.5m£¬AB=10m ”Ļ¦Į=30”ć£¬”Ļ¦Ā=60”ć |
AM=1.5m£¬AB=20m ”Ļ¦Į=30”ć£¬”Ļ¦Ā=60”ć |
|
| ¼ĘĖć¹ż³Ģ£Ø½į ¹ū±£ĮōøłŗÅ£© |
½ā£ŗ |
½ā£ŗ | |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| æĪĢā | ²āĮæŠ£ÄŚĘģøĖøß¶Č |
| ÄæµÄ | ŌĖÓĆĖłŃ§ŹżŃ§ÖŖŹ¶¼°ŹżŃ§·½·Ø½ā¾öŹµ¼ŹĪŹĢā--²āĮæĘģøĖøß¶Č |
| Ź¾ŅāĶ¼ | 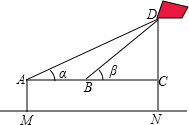 |
| ²āĮ湤¾ß | ʤ³ß”¢²ā½ĒŅĒ |
| ²āĮæŹż¾Ż£ŗ | AM=1.5m£¬AB=10m£¬”Ļ¦Į=30”ć£¬”Ļ¦Ā=60”ć |
| ¼ĘĖć¹ż³Ģ£Ø½į ¹ū±£ĮōøłŗÅ£© |
½ā£ŗ |
| ²āĮæ½į¹ū | DN= |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
| æĪĢā | ²āĮæŠ£ÄŚĘģøĖøß¶Č | ||
| ÄæµÄ | ŌĖÓĆĖłŃ§ŹżŃ§ÖŖŹ¶¼°ŹżŃ§·½·Ø½ā¾öŹµ¼ŹĪŹĢā----²āĮæĘģøĖøß¶Č | ||
| ·½°ø | ·½°øŅ» | ·½°ø¶ž | ·½°øČż |
Ź¾ŅāĶ¼ |  |  | |
| ²āĮ湤¾ß | ʤ³ß”¢²ā½ĒŅĒ | ʤ³ß”¢²ā½ĒŅĒ | |
| ²āĮæŹż¾Ż | AM=1.5m£¬AB=10m ”Ļ¦Į=30”ć£¬”Ļ¦Ā=60”ć | AM=1.5m£¬AB=20m ”Ļ¦Į=30”ć£¬”Ļ¦Ā=60”ć | |
| ¼ĘĖć¹ż³Ģ£Ø½į ¹ū±£ĮōøłŗÅ£© | ½ā£ŗ | ½ā£ŗ | |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗµŚ1ÕĀ”¶½āÖ±½ĒČż½ĒŠĪ”·ÖŠæ¼Ģā¼Æ£Ø35£©£ŗ1.5 ½āÖ±½ĒČż½ĒŠĪµÄÓ¦ÓĆ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
| æĪĢā | ²āĮæŠ£ÄŚĘģøĖøß¶Č | ||
| ÄæµÄ | ŌĖÓĆĖłŃ§ŹżŃ§ÖŖŹ¶¼°ŹżŃ§·½·Ø½ā¾öŹµ¼ŹĪŹĢā---²āĮæĘģøĖøß¶Č | ||
| ·½°ø | ·½°øŅ» | ·½°ø¶ž | ·½°øČż |
Ź¾ŅāĶ¼ | 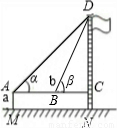 | 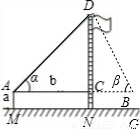 | |
| ²āĮ湤¾ß | ʤ³ß”¢²ā½ĒŅĒ | ʤ³ß”¢²ā½ĒŅĒ | |
| ²āĮæŹż¾Ż | AM=1.5m£¬AB=10m ”Ļ¦Į=30°£¬”Ļ¦Ā=60° | AM=1.5m£¬AB=20m ”Ļ¦Į=30°£¬”Ļ¦Ā=60° | |
| ¼ĘĖć¹ż³Ģ£Ø½į ¹ū±£ĮōøłŗÅ£© | ½ā£ŗ | ½ā£ŗ | |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com