
【题目】已知一次函数y=kx+b和反比例函数y=![]() 图象相交于A(2,4),B(n,﹣2)两点.
图象相交于A(2,4),B(n,﹣2)两点.
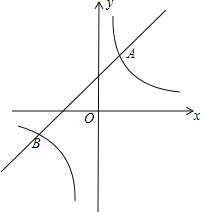
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出不等式kx+b﹣![]() <0的解集;
<0的解集;
(3)点C(a,b),D(a,c)(a>2)分别在一次函数和反比例函数图象上,且满足CD=2,求a的值.
【答案】(1)y=![]() ,y=x+2;(2)x<﹣4 或0<x<2;(3)a=2
,y=x+2;(2)x<﹣4 或0<x<2;(3)a=2![]() .
.
【解析】
(1)将点A坐标代入y=![]() 可用待定系数法求得反比例函数解析式,将B坐标代入所求解析式可求得n的值,再将A、B坐标代入y=kx+b用待定系数法求出一次函数解析式;
可用待定系数法求得反比例函数解析式,将B坐标代入所求解析式可求得n的值,再将A、B坐标代入y=kx+b用待定系数法求出一次函数解析式;
(2)由kx+b﹣![]() <0可得kx+b<
<0可得kx+b<![]() ,根据函数图象的性质分段讨论可求不等式kx+b﹣
,根据函数图象的性质分段讨论可求不等式kx+b﹣![]() <0的解集;
<0的解集;
(3)当a>2时,根据图象一次函数值大于反比例函数值,将点C,点D坐标代入函数解析式,求得C、D的纵坐标,又C、D的横坐标相同,所以CD等于C点纵坐标减去D点纵坐标,由此作答.
(1)∵反比例函数y=![]() 图象过点A(2,4),
图象过点A(2,4),
∴m=2×4=8,
∴反比例函数解析式为:y=![]() ,
,
∵点B在反比例函数图象上,
∴n=![]() =﹣4,
=﹣4,
∴点B(﹣4,﹣2),
根据题意得:![]() ,
,
解得:k=1,b=2,
∴一次函数解析式为:y=x+2;
(2)∵kx+b﹣![]() <0,
<0,
∴kx+b<![]() ,
,
∴一次函数图象在反比例函数图象的下方,
∴x<﹣4或0<x<2;
(3)∵点C(a,b),D(a,c)(a>2)分别在一次函数和反比例函数图象上,
∴b=a+2,c=![]() ,
,
∵CD=2,a>2,
∴a+2﹣![]() =2,
=2,
∴a=2![]() (负值已舍去).
(负值已舍去).


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4![]() ,则△CEF的周长为( )
,则△CEF的周长为( )
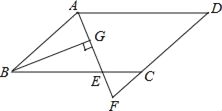
A.11.5B.10C.9.5D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李驾驶小汽车匀速地从A地行驶到B地,行驶里程为360千米,设小汽车的行驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
(1)求v关于t的函数表达式(不用写取值范围);
(2)小李上午8点驾驶小汽车从A地出发.
①小李需在当天12点至13点间到达B地,求小汽车行驶速度v的范围.
②小李能否在当天11点30分前到达B地?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网+”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用,名为“数据包络分析”(简称DEA)的一种效率评价方法,可以很好地优化出租车资源配置,为了解出租车资源的“供需匹配”,北京、上海等城市对每天24个时段的DEA值进行调查,调查发现,DEA值越大,说明匹配度越好.在某一段时间内,北京的DEA值y与时刻t的关系近似满足函数关系![]() (a,b,c是常数,且
(a,b,c是常数,且![]() ≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )
≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )
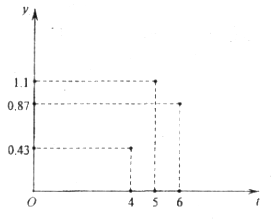
A. 4.8 B. 5 C. 5.2 D. 5.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F.
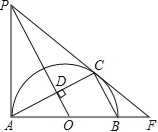
(1)求证:PC是半⊙O的切线;
(2)若∠CAB=30°,AB=10,求线段BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.

(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2,为什么?
(3)怎样围才能使围出的矩形场地面积最大?最大面积为多少?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
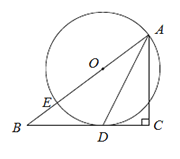
【题目】已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连结AD.
(1)求证:AD是∠BAC的平分线;
(2)若AC=3,BC=4,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com