
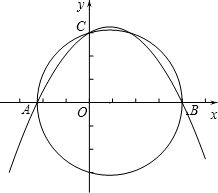
 如图,在平面直角坐标系xOy中,已知点A(-$\frac{9}{4}$,0),点C(0,3),点B是x轴上一点(位于点A的右侧,以AB为直径的圆恰好经过点C)
如图,在平面直角坐标系xOy中,已知点A(-$\frac{9}{4}$,0),点C(0,3),点B是x轴上一点(位于点A的右侧,以AB为直径的圆恰好经过点C)分析 (1)根据直径所对的圆周角是直角可以得到∠ACB是直角,再根据相似三角形的判定方法证明即可.
(2)利用三角形相似求出点B的坐标,然后根据A,B两点的坐标,重新假设抛物线的解析式,代入点C坐标求出a即可.
(3)分别以OB为底边和腰求出等腰三角形中点D的坐标.
解答 (1)证明:∵以AB为直径的圆恰好经过 点C,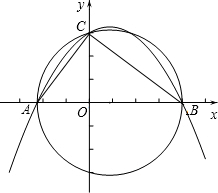
∴∠ACB=90°,
∵∠AOC=∠BOC=90°,
∴∠ACO+∠BCO=90°,∠BCO+∠CBO=90°,
∴∠ACO=∠CBO,
∴△△AOC∽△COB.
(2)∵△AOC∽△COB,
∴OC2=AO•OB,
∵A(-$\frac{9}{4}$,0),点C(0,3),
∴AO=$\frac{9}{4}$,OC=3,
又∵CO2=AO•OB,
∴32=$\frac{9}{4}$OB,
∴OB=4,
∴B(4,0),
∵抛物线经过B(4,0),A(-$\frac{9}{4}$,0),可以假设抛物线为y=a(x-4)(x+$\frac{9}{4}$),把(0,3)代入得a=-$\frac{1}{3}$
∴y=-$\frac{1}{3}$x2+$\frac{7}{12}$x+3.
(3)①OD=DB,如图:
D在OB 的中垂线上,过D作DH⊥OB,垂足是H,则H是OB中点.
Ⅴ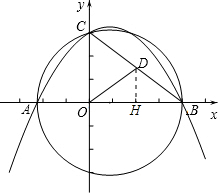
DH=$\frac{1}{2}$OC,OH=$\frac{1}{2}$OB,
∴D(2,$\frac{3}{2}$),
②BD=BO,如图: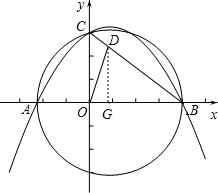
过D作DG⊥OB,垂足是G,
∴$\frac{BG}{OB}$=$\frac{BD}{CB}$=$\frac{DG}{OC}$,
∵OB=4,CB=5,
∴BD=OB=4,
∴$\frac{CD}{CB}$=$\frac{1}{5}$,
∴$\frac{BG}{4}$=$\frac{4}{5}$=$\frac{DG}{3}$,
∴BG=$\frac{16}{5}$,DG=$\frac{12}{5}$,
∴OG=BO-BG=$\frac{4}{5}$,
∴D( $\frac{4}{5}$,$\frac{12}{5}$).
点评 本题考查的是二次函数的综合题、圆的有关性质、相似三角形的判定和性质、等腰三角形的判定和性质,解题的关键是灵活应用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com