
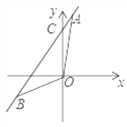
【题目】如图,直线a经过点A(1,6),和点B(﹣3,﹣2).
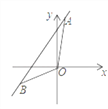
(1)求直线a的解析式;
(2)求直线与坐标轴的交点坐标;
(3)求S△AOB.
【答案】(1)y=2x+4;(2)交点坐标(﹣2,0)(0,4);(3)8.
【解析】分析:(1)设直线a的解析式为y=kx+b,用待定系数法求一次函数的解析式即可;(2)令x=0和y=0得出直线与坐标轴的交点坐标;(3)设直线a与有轴交于点C,根据S△AOB=S△AOC+S△COB得出答案即可.
本题解析:
(1)设直线a的解析式为y=kx+b,
∵直线a经过点A(1,6),和点B(﹣3,﹣2),
∴![]() ,解得
,解得![]() ,
,
∴直线a的解析式为y=2x+4;
(2)令x=0,得y=4; 令y=0得x=﹣2,
∴直线与坐标轴的交点坐标(﹣2,0)(0,4);
(3)设直线a与y轴交于点C,
∴S△AOB=S△AOC+S△COB=![]() ×4×3+
×4×3+![]() ×4×1=8.
×4×1=8.


科目:初中数学 来源: 题型:
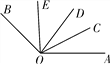
【题目】如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
(1)若∠AOB=160°,求∠COE的度数;
(2)若∠COE=75°,∠COA=20°,求∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O的半径为5cm,弦AB//CD , 且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
A.1 cm
B.7cm
C.3 cm或4 cm
D.1cm 或7cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是( )
A.(-2,6)
B.(-2,0)
C.(1,3)
D.(-5,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com