
 如图,已知直线y=-$\frac{1}{2}$x+2与坐标轴交于A、B两点,抛物线y=-x2+bx+c与x轴交于A、C两点,与y轴交于点B.
如图,已知直线y=-$\frac{1}{2}$x+2与坐标轴交于A、B两点,抛物线y=-x2+bx+c与x轴交于A、C两点,与y轴交于点B.分析 (1)因为直线y=-$\frac{1}{2}$x+2与坐标轴交于A、B两点,所以可得A(4,0),B(0,2),把A(4,0),B(0,2)代入y=-x2+bx+c得:$\left\{\begin{array}{l}{-16+4b+c=0}\\{c=2}\end{array}\right.$,解得;$\left\{\begin{array}{l}{b=\frac{7}{2}}\\{c=2}\end{array}\right.$.
(2)①当x=2时,求出D,E的纵坐标,从而得到DE=4,又因为P(t,0),所以可得F(t,$-\frac{1}{2}t$+2),G(t,$-{t}^{2}+\frac{7}{2}t$+2),所以FG=$|-{t}^{2}+\frac{7}{2}t+2-(-\frac{1}{2}t+2)|$=|-t2+4t|,根据FG:DE=1:2,得到FG=|-t2+4t|=2,解方程,即可解答;
(3)过点E′作E′H⊥y轴于H,则E′H=2,易证:OB′=B′E′,由题意得点B′(0,2+m),点E′(2,5+m),在Rt△E′H B′中,B′E′=OB′=2+m,B′H=5+m-(2+m)=3,利用勾股定理得到B′E′=$\sqrt{{2}^{2}+{3}^{2}}=\sqrt{13}$,所以m=$\sqrt{13}-2$.
解答 解:(1)∵直线y=-$\frac{1}{2}$x+2与坐标轴交于A、B两点,
∴A(4,0),B(0,2),
把A(4,0),B(0,2)代入y=-x2+bx+c得:
$\left\{\begin{array}{l}{-16+4b+c=0}\\{c=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=\frac{7}{2}}\\{c=2}\end{array}\right.$.
抛物线的解析式为:y=$-{x}^{2}+\frac{7}{2}x+2$
(2)①当x=2时,yD=$-\frac{1}{2}×2+2$=1,yE=$-{2}^{2}+\frac{7}{2}×2+2$=5,
∴DE=4
又∵P(t,0),
∴F(t,$-\frac{1}{2}t$+2),G(t,$-{t}^{2}+\frac{7}{2}t$+2),
∴FG=$|-{t}^{2}+\frac{7}{2}t+2-(-\frac{1}{2}t+2)|$=|-t2+4t|,
∵FG:DE=1:2,
∴FG=|-t2+4t|=2,
解得:$t=2±\sqrt{2}$或t=$2±\sqrt{6}$(负根舍去)
∴当t=$2±\sqrt{2}$或t=$2+\sqrt{6}$时,FG:DE=1:2;
②如图,过点E′作E′H⊥y轴于H,则E′H=2,
∵E′O平分∠B′E′D,
∴∠B′E′O=∠OE′D,
又∵OH∥DE′,
∴∠B′OE′=∠OE′D,
∴∠B′E′O=∠B′OE′
∴OB′=B′E′,
由题意得点B′(0,2+m),点E′(2,5+m),
在Rt△E′H B′中,B′E′=OB′=2+m,
B′H=5+m-(2+m)=3,
∴B′E′=$\sqrt{{2}^{2}+{3}^{2}}=\sqrt{13}$,
∴m=$\sqrt{13}-2$.
点评 本题考查了二次函数,解决本题的关键是求出F,G点的坐标,以及数形结合思想的应用.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
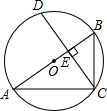 如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )| A. | 6 | B. | $2\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com