
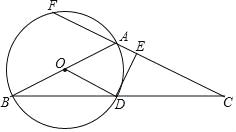
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE⊥AC;
(2)若DE+EA=8,⊙O的半径为10,求AF的长度.
【答案】(1)证明见解析(2)8
【解析】
试题分析:(1)欲证明DE⊥AC,只需推知OD∥AC即可;
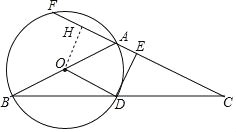
(2)如图,过点O作OH⊥AF于点H,构建矩形ODEH,设AH=x.则由矩形的性质推知:AE=10﹣x,OH=DE=8﹣(10﹣x)=x﹣2.在Rt△AOH中,由勾股定理知:x2+(x﹣2)2=102,通过解方程得到AH的长度,结合OH⊥AF,得到AF的值.
试题解析:(1)∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC.
∵DE是⊙O的切线,OD是半径,
∴DE⊥OD,
∴DE⊥AC;
(2)如图,过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,
∴四边形ODEH是矩形,
∴OD=EH,OH=DE.
设AH=x.
∵DE+AE=8,OD=10,
∴AE=10﹣x,OH=DE=8﹣(10﹣x)=x﹣2.
在Rt△AOH中,由勾股定理知:AH2+OH2=OA2,即x2+(x﹣2)2=102,
解得x1=8,x2=﹣6(不合题意,舍去).
∴AH=8.
∵OH⊥AF,
∴AH=FH=![]() AF,
AF,
∴AF=2AH=2×8=16.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】折纸的思考.
【操作体验】
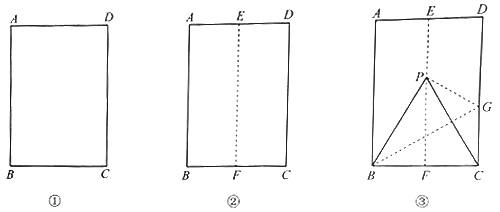
用一张矩形纸片折等边三角形.
第一步,对折矩形纸片![]() (图①),使
(图①),使![]() 与
与![]() 重合,得到折痕
重合,得到折痕![]() ,把纸片展平(图②).
,把纸片展平(图②).
第二步,如图③,再一次折叠纸片,使点![]() 落在
落在![]() 上的
上的![]() 处,并使折痕经过点
处,并使折痕经过点![]() ,得到折痕
,得到折痕![]() ,折出
,折出![]() ,得到
,得到![]() .
.
(1)说明![]() 是等边三角形.
是等边三角形.
【数学思考】
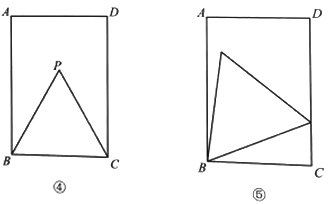
(2)如图④.小明画出了图③的矩形![]() 和等边三角形
和等边三角形![]() .他发现,在矩形
.他发现,在矩形![]() 中把
中把![]() 经过图形变化,可以得到图⑤中的更大的等边三角形.请描述图形变化的过程.
经过图形变化,可以得到图⑤中的更大的等边三角形.请描述图形变化的过程.
(3)已知矩形一边长为3![]() ,另一边长为
,另一边长为![]() .对于每一个确定的
.对于每一个确定的![]() 的值,在矩形中都能画出最大的等边三角形.请画出不同情形的示意图,并写出对应的
的值,在矩形中都能画出最大的等边三角形.请画出不同情形的示意图,并写出对应的![]() 的取值范围.
的取值范围.
【问题解决】
(4)用一张正方形铁片剪一个直角边长分别为4![]() 和1
和1![]() 的直角三角形铁片,所需正方形铁片的边长的最小值为
的直角三角形铁片,所需正方形铁片的边长的最小值为 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:6cos45°+(![]() )﹣1+(
)﹣1+(![]() ﹣1.73)0+|5﹣3
﹣1.73)0+|5﹣3![]() |+42017×(﹣0.25)2017
|+42017×(﹣0.25)2017
(2)先化简,再求值:(![]() ﹣a+1)÷
﹣a+1)÷![]() ﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,是随机事件的是( )
A.三角形任意两边之和大于第三边
B.任意选择某一电视频道,它正在播放新闻联播
C.a是实数,|a|≥0
D.在一个装着白球和黑球的袋中摸球,摸出红球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解游客在十渡、周口店北京人遗址博物馆、圣莲山和石花洞这四个风景区旅游的满意率,数学小组的同学商议了几个收集数据的方案:
方案一:在多家旅游公司调查400名导游;
方案二:在十渡风景区调查400名游客;
方案三:在云居寺风景区调查400名游客;
方案四:在上述四个景区各调查100名游客.
其中,最合理的收集数据的方案是( )
A.方案一B.方案二C.方案三D.方案四
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个商店把彩电按标价的九折出售,仍可获利20%,若该彩电的进价是2400元,则彩电标价是( )
A.3200元B.3429元C.2667元D.3168元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com