
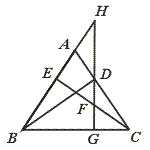
科目:初中数学 来源:不详 题型:单选题
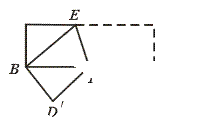
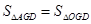 ;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有 ( ▲ )
;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有 ( ▲ )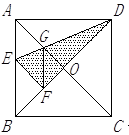
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.36cm2 | B.85 cm2 | C.96 cm2 | D.100 cm2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A.4 cm、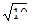 cm cm | B.5 cm、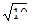 cm cm |
C.4 cm、2 cm cm | D.5 cm、2 cm cm |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
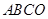 的边
的边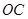 落在
落在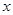 轴的正半轴上,且
轴的正半轴上,且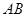 ∥
∥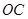 ,
,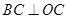 ,
,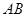 =4,
=4,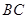 =6,
=6,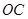 =8.正方形
=8.正方形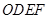 的两边分别落在坐标轴上,且它的面积等于直角梯形
的两边分别落在坐标轴上,且它的面积等于直角梯形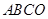 面积。将正方形
面积。将正方形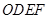 沿
沿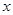 轴的正半轴平行移动,设它与直角梯形
轴的正半轴平行移动,设它与直角梯形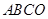 的重叠部分面积为
的重叠部分面积为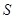 。
。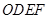 的边长;
的边长;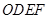 平行移动过程中,通过操作、观察,试判断
平行移动过程中,通过操作、观察,试判断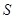 (
(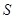 >0)的变化情况是 ;
>0)的变化情况是 ;| A.逐渐增大 | B.逐渐减少 | C.先增大后减少 | D.先减少后增大 |
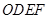 顶点
顶点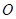 移动到点
移动到点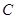 时,求
时,求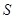 的值;
的值;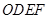 的顶点
的顶点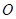 向右移动的距离为
向右移动的距离为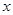 ,求重叠部分面积
,求重叠部分面积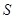 与
与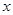 的函数关系式。
的函数关系式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com