
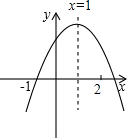
 已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有①③④.
已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有①③④. 分析 由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①由图象可知:a<0,c>0,
∵-$\frac{b}{2a}$>0,
∴b>0,
∴abc<0,故此选项正确;
②当x=-1时,y=a-b+c<0,故a+c>b,错误;
③当x=3时函数值小于0,y=9a+3b+c<0,且x=-$\frac{b}{2a}$=1,
即b=-2a,代入得9a-6a+c<0,得3a+c<0,故此选项正确;
④当x=1时,y的值最大.此时,y=a+b+c,
而当x=m时,y=am2+bm+c,
所以a+b+c>am2+bm+c,
故a+b>am2+bm,即a+b>m(am+b),故此选项正确.
故①③④正确.
故答案为:①③④.
点评 本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为一条抛物线,当a<0,抛物线的开口向下,当x=-$\frac{b}{2a}$时,函数值最大;抛物线与y轴的交点坐标为(0,c).


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | 8 | C. | $\frac{1}{8}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
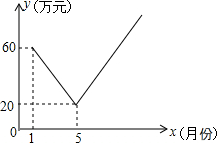 保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2016年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月利润60万元逐月等额下降,到5月份利润为20万元.5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.
保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2016年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月利润60万元逐月等额下降,到5月份利润为20万元.5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
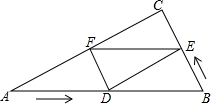 如图,△ABC中,∠C=90°,BC=5,AC=5$\sqrt{3}$,点D从A出发沿AB以每秒2个单位的速度向点B匀速运动,同时,点E从B出发沿BC以每秒1个单位的速度向点C匀速运动.当一个点到达终点时,另一个点也停止运动.设点D、E运动的时间为t(t>0),作DF⊥AC于F,连DE、EF.
如图,△ABC中,∠C=90°,BC=5,AC=5$\sqrt{3}$,点D从A出发沿AB以每秒2个单位的速度向点B匀速运动,同时,点E从B出发沿BC以每秒1个单位的速度向点C匀速运动.当一个点到达终点时,另一个点也停止运动.设点D、E运动的时间为t(t>0),作DF⊥AC于F,连DE、EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩/分 | 80 | 85 | 90 | 95 |
| 人数/人 | 1 | 2 | 5 | 2 |
| A. | 90,89 | B. | 90,90 | C. | 85,89 | D. | 90,87.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
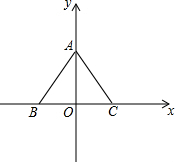 如图,△ABC在平面直角坐标系中的位置如图所示,若S△ABC=12,BC=2OC,且AC,BC的长满足$\left\{\begin{array}{l}{BC-AC=1}\\{BC+AC=11}\end{array}\right.$.
如图,△ABC在平面直角坐标系中的位置如图所示,若S△ABC=12,BC=2OC,且AC,BC的长满足$\left\{\begin{array}{l}{BC-AC=1}\\{BC+AC=11}\end{array}\right.$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com