
【题目】如图:![]() 是
是![]() 的直径,
的直径,![]() 是弦,
是弦,![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接DO,由三角形的外角与内角的关系可得∠DOC=∠C=45°,故有∠ODC=90°,即CD是圆的切线.
(2)由(1)可得![]() OCD是等腰直角三角形,再根据勾股定理得出OC的长,再根据BC=OC﹣OB即可.
OCD是等腰直角三角形,再根据勾股定理得出OC的长,再根据BC=OC﹣OB即可.
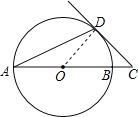
(1)证明:连接DO,
∵AO=DO,
∴∠DAO=∠ADO=22.5°.
∴∠DOC=45°.
又∵∠ACD=2∠DAB,
∴∠ACD=∠DOC=45°.
∴∠ODC=90°.
又 OD是⊙O的半径,
∴CD是⊙O的切线.
(2)连接DB,
∵∠ACD=∠DOC=45°, ∴CD=OD
∵直径AB=2![]() ,
,
∴CD=OD=![]() ,OC=
,OC=![]() =2,
=2,
∴BC=OC﹣OB=2﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,则下列五个结论中:①albic<0;②a﹣b+c>0;③2a﹣b<0;④abc<0;⑤4a+2b+c>0,错误的个数有( )
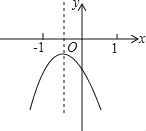
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40 cm,这个三角形的面积S(单位:cm2)随x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,这个三角形面积S最大?最大面积是多少?![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电脑键盘上的字母为何不按顺序排列?请你来做一项统计,下面是一篇小短文,根据短文中字母a,b出现的机会完成后面提出的问题:
Two Trips
Jack brought a small plane and began to fly it. He soon became excited and made his plane all kinds of tricks.
Jack had a friend,named Tom. One day Jack said to him,“I will pick you up in my plane.““I will be glad to.'answered Tom. They went up,and Jack flew around for half an hour and did all kinds of tricks in the air. Then they came down. Tom was to be back safely,and said to Jack,“Well,Jack,thank you very much for those two trips in your plane.“Jack was very surprised and asked,“Two trips?““Yes,my first and my last.'an﹣swered Tom.
根据上文填表
出现字母的个数 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
出现字母a的频数 | |||||||
出现字母a的频率 | |||||||
出现字母b的频数 | |||||||
出现字母b的频率 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(a,﹣![]() )在直线y=﹣
)在直线y=﹣![]() 上,AB∥y轴,且点B的纵坐标为1,双曲线y=
上,AB∥y轴,且点B的纵坐标为1,双曲线y=![]() 经过点B.
经过点B.
(1)求a的值及双曲线y=![]() 的解析式;
的解析式;
(2)经过点B的直线与双曲线y=![]() 的另一个交点为点C,且△ABC的面积为
的另一个交点为点C,且△ABC的面积为![]() .
.
①求直线BC的解析式;
②过点B作BD∥x轴交直线y=﹣![]() 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
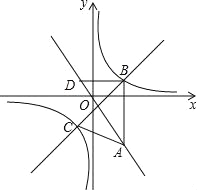
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为10,则GE+FH的最大值为( )
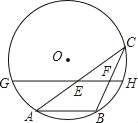
A. 5 B. 10 C. 15 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
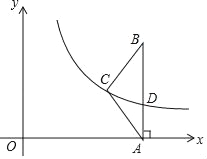
【题目】如图,在△ABC中,AC=BC=5,AB=8,AB⊥x轴,垂足为A,反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.
(x>0)的图象经过点C,交AB于点D.
(1)若OA=AB,求k的值;
(2)若BC=BD,连接OC,求△OAC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com