
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径.点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
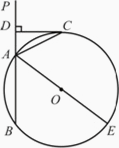
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
|
(1)证明:连接OC, 因为点C在⊙O上,0A=OC,所以∠OCA=∠OAC,因为CD⊥PA,所以∠CDA=90°, 有∠CAD+∠DCA=90°,因为AC平分∠PAE,所以∠DAC=∠CAO. 所以∠DC0=∠DCA+∠ACO=∠DCA+∠CAO=∠DCA+∠DAC=90°. 又因为点C在⊙O上,OC为⊙0的半径,所以CD为⊙0的切线. (2)解:过O作0F⊥AB,垂足为F,所以∠OCA=∠CDA=∠OFD=90°,
所以四边形OCDF为矩形,所以0C=FD,OF=CD. ∵DC+DA=6,设AD=x,则OF=CD=6-x, ∵⊙O的直径为10,∴DF=OC=5,∴AF=5-x, 在Rt△AOF中,由勾股定理得 即 解得 由AD<DF,知 从而AD=2,AF=5-2=3. ∵OF⊥AB,由垂径定理知,F为AB的中点,∴AB=2AF=6. |


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
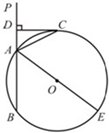 23、如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD丄PA,垂足为D.
23、如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD丄PA,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:
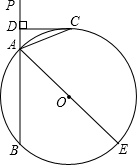 (2012•昌平区一模)如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,C为⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA于D.
(2012•昌平区一模)如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,C为⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA于D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(安徽芜湖卷)数学 题型:解答题
(本小题满分12分)
如图,已知直线PA交⊙0于A、B两点,AE是⊙0的直径.点C为⊙0上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D。
(1)求证:CD为⊙0的切线;
(2)若DC+DA=6,⊙0的直径为l0,求AB的长度.
查看答案和解析>>
科目:初中数学 来源:2012届北京门头沟中考二模数学试卷(带解析) 题型:解答题
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径.点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
【小题1】求证:CD为⊙O的切线;
【小题2】若DC+DA=6,⊙O的直径为10,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com