
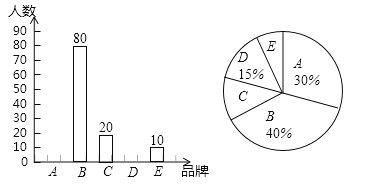
【题目】“共享单车,绿色出行”,现如今骑共享单车出行不但成为一种时尚,也称为共享经济的一种新形态,某校九(1)班同学在街头随机调查了一些骑共享单车出行的市民,并将他们对各种品牌单车的选择情况绘制成如下两个不完整的统计图(A:摩拜单车;B:ofo单车;C:HelloBike).请根据图中提供的信息,解答下列问题:
(1)求出本次参与调查的市民人数;
(2)将上面的条形图补充完整;
(3)若某区有10000名市民骑共享单车出行,根据调查数据估计该区有多少名市民选择骑摩托单车出行?
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点
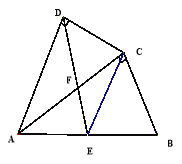
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张翔上午7:30出发,从学校骑自行车去县城,路程全长20km,中途因道路施工步行一段路.他步行的平均速度是5km/h
(1)若张翔骑车的平均速度是15km/h,当天上午9:00到达县城,则他骑车与步行各用多少时间?
(2)若张翔必须在当天上午9:00之前赶到县城,他的步行平均速度不变,则他骑车的平均速度应在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
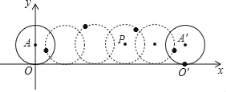
【题目】如图,在平面直角坐标系中,半径为1的圆从原点出发沿x轴正方向滚动一周,圆上一点由原点O到达点O′,圆心也从点A到达点A′.
(1)点O′的坐标为 ,点A′的坐标为 ;
(2)若点P是圆在滚动过程中圆心经过的某一位置,求以点P,点O,点O′为顶点的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如下(未完成),解答下列问题:
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中D小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
在解方程组或求代数式的值时,可以用整体代入或整体求值的方法,化难为易.
(1)解方程组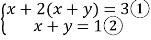
(2)已知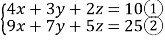 ,求x+y+z的值
,求x+y+z的值
解:(1)把②代入①得:x+2×1=3.解得:x=1.
把x=1代入②得:y=0.
所以方程组的解为![]() ,
,
(2)①×2得:8x+6y+4z=20.③
②﹣③得:x+y+z=5.
(类比迁移)
(1)若![]() ,则x+2y+3z= .
,则x+2y+3z= .
(2)解方程组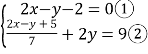
(实际应用)
打折前,买39件A商品,21件B商品用了1080元.打折后,买52件A商品,28件B商品用了1152元,比不打折少花了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(3,0),B(0,1)

(1)将△ABC沿x轴的正方向平移t个单位,B、C两点的对应点B′、C′正好落在反比例函数y=![]() 的图象上.请直接写出C点的坐标和t,k的值;
的图象上.请直接写出C点的坐标和t,k的值;
(2)有一个Rt△DEF,∠D=90°,∠E=60°,DE=2,将它放在直角坐标系中,使斜边EF在x轴上,直角顶点D在(1)中的反比例函数图象上,求点F的坐标;
(3)在(1)的条件下,问是否存在x轴上的点M和反比例函数y=![]() 图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,E为对角线BD的延长线上一点.

(1)求证:AE=CE.
(2)若BC=6,AE=10,∠BAE=120,求BE的长,并直接写出DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.

(1)已知:如图1,四边形ABCD的顶点A,B,C在网格格点上,请你在如下的5![]() 7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
(2)如图2,矩形ABCD中,AB=![]() ,BC=5,点E在BC边上,连结DE画AF
,BC=5,点E在BC边上,连结DE画AF![]() DE于点F,若DE=
DE于点F,若DE=![]() CD,找出图中的等邻边四边形;
CD,找出图中的等邻边四边形;
(3)如图3,在Rt![]() ABC中,
ABC中,![]() ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com