
已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系?为什么?
②求∠ODC的度数.
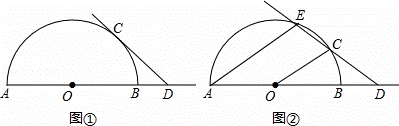
解:(1)如图①,连接OC,
∵OC=OA,CD=OA,
∴OC=CD,
∴∠ODC=∠COD,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ODC=45°;
(2)如图②,连接OE.
∵CD=OA,∴CD=OC=OE=OA,
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠ODC=∠1=x,则∠2=∠3=∠4=x.
∴∠AOE=∠OCD=180°﹣2x.
①AE=OD.理由如下:
在△AOE与△OCD中,

∴△AOE≌△OCD(SAS),
∴AE=OD.
②∠6=∠1+∠2=2x.
∵OE=OC,∴∠5=∠6=2x.
∵AE∥OC,
∴∠4+∠5+∠6=180°,即:x+2x+2x=180°,
∴x=36°.
∴∠ODC=36°.




科目:初中数学 来源: 题型:
某校为了解该校九年级学生对蓝球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况,对九年级部分学生进行了随机抽样调查,每名学生必须且只能选择最喜爱的一项运动项目上,将调查结果统计后绘制成如图两幅不完整的统计图,请根据图中的信息,回答下列问题:
(1)这次被抽查的学生有 ”对应扇形的圆心角是 度;
(3)若该校九年级共有480名学生,估计该校九年级最喜欢足球的学生约有 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,是某公园的一角,∠AOB=90°, 的半径OA长是6米,点C是OA的中点,点D在
的半径OA长是6米,点C是OA的中点,点D在 上,CD∥OB,则图中草坪区(阴影部分)的面积是( )
上,CD∥OB,则图中草坪区(阴影部分)的面积是( )

|
| A. | (3π+ | B. | ( | C. | (3π+9 | D. | ( |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com