
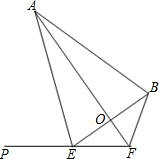
 (2013•石景山区二模)如图,四边形ABFE中,延长FE至点P,∠AEP=74°,∠BEF=30°,∠EFB=120°,AF平分∠EFB,EF=2.求AB长(结果精确到0.1).
(2013•石景山区二模)如图,四边形ABFE中,延长FE至点P,∠AEP=74°,∠BEF=30°,∠EFB=120°,AF平分∠EFB,EF=2.求AB长(结果精确到0.1).| 3 |
| 2 |
| 3 |
| 3 |
| OE |
| cos∠AEO |
| ||
| cos76° |
|


科目:初中数学 来源: 题型:
(2013•石景山区二模)一射击运动员在一次射击练习中打出的成绩如下表所示:这次成绩的众数、平均数是( )
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com