
【题目】如图,平行四边形ABCD的对角线相交于点O,过点O的任意一条直线与边AD相交于点E,与边BC相交于点F,求证:OE=OF. 
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在图①中的正方形中剪去一个边长为2a+b的正方形,将剩余的部分按图②的方式拼成一个长方形.
(1)求剪去正方形的面积;
(2)求拼成的长方形的长、宽以及它的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( ) 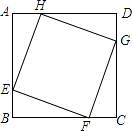
A.30
B.34
C.36
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
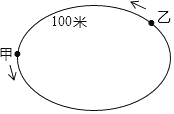
【题目】已知甲沿周长为300米的环形跑道按逆时针方向跑步,速度为a米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.
(1)若a=1,求甲、乙两人第一次相遇所用的时间;
(2)若a>3,甲、乙两人第一次相遇所用的时间为80秒,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2-6n+9=0,求m和n的值.
∵m2+2mn+2n2-6n+9=0
∴m2+2mn+n2+n2-6n+9=0
∴(m+n)2+(n-3)2=0
∴m+n=0,n-3=0
∴m=-3,n=3
问题(1)若x2+2y2-2xy-4y+4=0,求xy的值.
(2)已知a,b,c是△ABC的三边长,满足a2+b2-6a-6b+18+| 3-c |=0,请问△ABC是怎样形状的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某网店的“翻牌抽奖”活动,如图,共有4张牌,分别对应5元,10元,15元,20元的现金优惠券,小明只能看到牌的背面. 
(1)如果随机翻一张牌,那么抽中20元现金优惠券的概率是 .
(2)如果随机翻两张牌,且第一次翻的牌不参与下次翻牌,则所获现金优惠券的总值不低于30元的概率是多少?请画树状图或列表格说明问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,求证:∠ACD=∠B;
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状?并说明理由?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,点C,B,E在同一直线上,若AB⊥BD,AB=BD,则CE与AC,DE有什么等量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com