
【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
分数段 | 频数 | 频率 |
60≤x<70 | 40 | 0.40 |
70≤x<80 | 35 | b |
80≤x<90 | a | 0.15 |
90≤x<100 | 10 | 0.10 |
频率分布统计表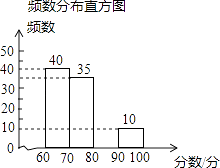
请根据上述信息,解答下列问题:
(1)分别求出a、b的值;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数.
【答案】
(1)
解:总的调查人数= ![]() =100人,
=100人,
∵第二组的频数为35,
∴b= ![]() =0.35;
=0.35;
∵第三组的频率为0.15,
∴a=100×0.15=15.
(2)
解:补全频数分布直方图如下所示;

(3)
解:优秀率=(0.15+0.10)×100%=25%,
1500×25%=375(人).
【解析】(1)根据第一组的频数与频率可求出总的调查人数,然后根据第二组的频数和第三组的频率即可求出a和b的值;(2)根据(1)中求出的a值,可补全频数分布直方图;(3)优秀率=第三组和第四组的频率之和×100%;用总人数乘以优秀率,计算即可得解.
【考点精析】本题主要考查了频数分布直方图的相关知识点,需要掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】随着科学技术的不断进步,我国海上能源开发和利用已达到国际领先水平.下图为我国在南海海域自主研制的海上能源开发的机器装置AB,一直升飞机在离海平面l距离为150米的空中点P处,看到该机器顶部点A处的俯角为38°,看到露出海平面的机器部分点B处的俯角为65°,求这个机器装置露出海平面部分AB的高度?(结果精确到0.1,参考数据:sin65°=0.9063,sin38°=0.6157,tan38°=0.7813,tan65°=2.1445.)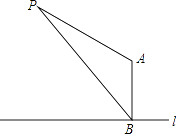
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂分别安排甲乙两个车间加工1000个同一型号的奥运会吉祥物,每名工人每天加工吉祥物的个数相等且保持不变,由于生产需要,其中一个车间推迟两天开始加工,刚开始加工时,甲车间有10名工人,乙车间有12名工人,图中线段OB和折线ACB分别表示两个车间的加工情况.依据图中提供的信息,完成下列各题:
(1)线段OB反映的是 车间的加工情况;
(2)开始加工后,甲车间加工多少天后,两车间加工吉祥物数相同?
(3)根据折线段反映的加工情况,请你提出一个问题,并给出解答.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2,﹣1),交x轴于点A、B两点,交y轴于点C,其中点B的坐标为(3,0).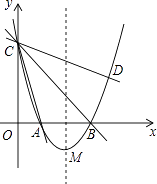
(1)求抛物线的解析式;
(2)设经过点C的直线与该抛物线的另一个点为D,且直线CD和直线CA关于直线CB对称,求直线CD的解析式;
(3)在该抛物线的对称轴上存在点P,满足PM2+PB2+PC2=35,求点P的坐标;并直接写出此时直线OP与该抛物线交点的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2012年6月3号国际田联钻石联赛美国尤金站比赛中,百米跨栏飞人刘翔以12.87s的成绩打破世界记录并轻松夺冠.A、B两镜头同时拍下了刘翔冲刺时的画面(如图),从镜头B观测到刘翔的仰角为60°,从镜头A观测到刘翔的仰角为30°,若冲刺时的身高大约为1.88m,请计算A、B两镜头之间的距离为 . (结果保留两位小数, ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)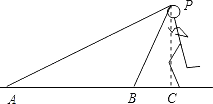
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,O为对角线AC的中点,EF经过点O并与AB,CD分别相交于点E,F.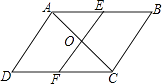
(1)求证:AE=CF;
(2)当EF⊥AC时,连接AF,CE,试判断四边形AFCE是怎样的四边形?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com