练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．一辆货车从超市出发，向东走了3km，到达小刚家，继续向东走了4km到达小红家，又向西走了9km到达小英家，最后回到超市．
    （1）请以超市为原点，以向东方向为正方向，用1个单位长度表示1km，画出数轴．并在数轴上表示出小刚家、小红家、小英家的位置；
    （2）货车一共行驶了多少千米？

    分析 （1）以超市为原点，以向东方向为正方向，用1个单位长度表示1km，依此画出数轴．并在数轴上表示出小刚家、小红家、小英家的位置；
    （2）根据已知图象，注意要用绝对值来表示距离进而得出答案．

    解答 解：（1）如图所示：
    ；

    （2）货车一共行驶了：2+3+9+4=18（千米），
    答：货车一共行驶了18千米．

    点评 本题主要考查了数轴在实际生活中的应用，注意表示距离要用绝对值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．如图，矩形ABCD．AE=CD，DF⊥BE于F．求证：∠E=∠ADF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下面说法中正确的是（　　）
    A．因为同号相乘得正，所以（-2）×（-3）×（-1）=6
    B．任何数和0相乘都等于0
    C．若a×b＞0，则a＞0，b＞0
    D．以上说法都不正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列事件中，是必然事件的是（　　）
    A．任意抛掷一枚硬币，出现正面
    B．从2、4、6、8、10这5张卡片中任抽一张是奇数
    C．从装有一个红球三个黄球的袋子中任取两球，至少有一个是黄球
    D．投掷一枚普通骰子，朝上一面的点数是3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．若x，y均为正整数，且2x•4y=32，则x+y的值为3或4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算．
    （1）3-（+5）-|-2|
    （2）-16×4÷（-1$\frac{3}{5}$）
    （3）23-6×（-3）+2×（-4）
    （4）（-0.5）-（-3$\frac{1}{4}$）+2.75-（-7$\frac{1}{2}$）
    （5）（$\frac{5}{12}$+$\frac{2}{3}$-$\frac{3}{4}$）×（-12）
    （6）-32-$\frac{1}{3}$×[（-5）2×（-$\frac{3}{5}$）-240÷（-4）×$\frac{1}{4}$]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知y关于x的一次函数图象上的两点为（0，8）和（-1，2）．
    （1）求此一次函数表达式；
    （2）当1＜x＜4时，求y的取值范围；
    （3）当-3＜y＜3时，求x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．阅读材料题：如果x1，x2是一元二次方程ax2+bx+c=0的两个根，那么x1+x2=$-\frac{b}{a}$，${x_1}．{x_2}=\frac{c}{a}$．这是一元二次方程根与系数的关系，我们利用它可以来计算某些代数式的值．
    例：x1，x2是方程x2+6x-3=0的两个根，求$x_1^2+x_2^2$的值．
    可以这样求解：∵x1+x2=-6，x1x2=-3，
    ∴$x_1^2+x_2^2$=（x1+x2）2-2x1x2=（-6）2-2×（-3）=42
    请你根据以上解答完成下列问题：
    已知x1，x2是方程x2-4x+2=0的两根，分别求下列代数式的值．
    （1）（x1+1）（x2+1）的值；       
    （2）$\frac{1}{x_1}+\frac{1}{x_2}$的值；       
    （3）x1x${\;}_{2}^{2}$+x${\;}_{1}^{2}$x2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

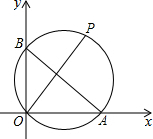    20．如图，已知A、B两点的坐标分别为（4，0）、（0，3），P是△AOB外接圆上的一点，且∠AOP=45°，则点P的坐标为（$\frac{7}{2}$，$\frac{7}{2}$）或（$\frac{1}{2}$，-$\frac{1}{2}$）．

    查看答案和解析>>

    同步练习册答案