
【题目】如图,二次函数y2=ax2+bx+3的图象与x轴相交于点A(3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y1=mx+n的图象经过B. D两点.
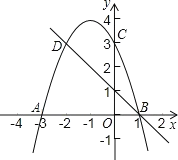
(1)求a、b的值及点D的坐标;
(2)根据图象写出y2>y1时,x的取值范围.
【答案】(1)a=-1,b=-2, D(-2,3);(2)2<x<0
【解析】
(1)由于已知抛物线与x轴的交点坐标,则设交点式y=a(x+3)(x-1)=![]() ,则-3a=3,解得a=-1,所以b=-2,抛物线的对称轴为直线x=-1,再求出C点坐标为(0,3),然后根据对称的性质确定D点坐标为(-2,3);
,则-3a=3,解得a=-1,所以b=-2,抛物线的对称轴为直线x=-1,再求出C点坐标为(0,3),然后根据对称的性质确定D点坐标为(-2,3);
(2)观察函数图象得到当-2<x<0时,抛物线都在直线y=mx+n的上方,即y2>y1.
(1)设抛物线解析式为y=a(x+3)(x1)= ![]() ,
,
则3a=3,解得a=1,
所以抛物线解析式为y=![]() ;
;
所以b=2,
抛物线的对称轴为直线x=1,
当x=0时, ![]() ,则C点坐标为(0,3),
,则C点坐标为(0,3),
由于C. D是二次函数图象上的一对对称点,
∴D点坐标为(2,3);
(2)观察函数图象得到当-2<x<0时,抛物线都在直线y=mx+n的上方,即y2>y1.当2<x<0时, ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
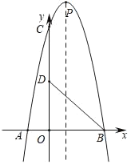
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+8与x轴相交于点A(﹣2,0)和点B(4,0),与y轴相交于点C,顶点为点P.点D(0,4)在OC上,联结BC、BD.
(1)求抛物线的表达式并直接写出点P的坐标;
(2)点E为第一象限内抛物线上一点,如果△COE与△BCD的面积相等,求点E的坐标;
(3)点Q在抛物线对称轴上,如果△BCD∽△CPQ,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上,若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长度始终相等?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
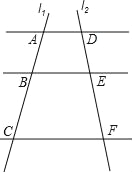
【题目】如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,![]() ,AC=14;
,AC=14;
(1)求AB、BC的长;
(2)如果AD=7,CF=14,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
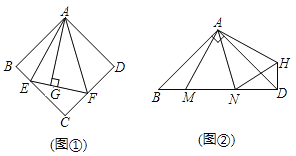
【题目】![]() 如图
如图![]() ,在正方形ABCD中,
,在正方形ABCD中,![]() 的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求
的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求![]() 的度数.
的度数.
![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,点M,N是BD边上的任意两点,且
,点M,N是BD边上的任意两点,且![]() ,将
,将![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() 至
至![]() 位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
![]() 在图
在图![]() 中,连接BD分别交AE,AF于点M,N,若
中,连接BD分别交AE,AF于点M,N,若![]() ,
,![]() ,
,![]() ,求AG,MN的长.
,求AG,MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:已知实数m,n满足(2m2+n2+1)(2m2+n2﹣1)=80,试求2m2+n2的值
解:设2m2+n2=t,则原方程变为(t+1)(t﹣1)=80,整理得t2﹣1=80,t2=81,∴t=±9因为2m2+n2≥0,所以2m2+n2=9.
上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
已知实数x,y满足(4x2+4y2+3)(4x2+4y2﹣3)=27,求x2+y2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com