
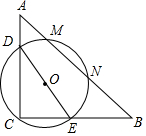
 如图,在Rt△ACB中,∠ACB=90°,AC=6,BC=8,D,E分别在AC,BC上,且DE=6,以DE为直径的⊙O 交AB于点M,N,则弦长MN的最大值为( )
如图,在Rt△ACB中,∠ACB=90°,AC=6,BC=8,D,E分别在AC,BC上,且DE=6,以DE为直径的⊙O 交AB于点M,N,则弦长MN的最大值为( )| A. | 2.4 | B. | 4.8 | C. | 5 | D. | 6 |
分析 根据题意有C、O、G三点在一条直线上OG最小,MN最大,根据勾股定理求得AB,根据三角形面积求得CF,然后根据垂径定理和勾股定理即可求得MN的最大值.
解答 解:过O作OG⊥AB于G,连接OC,连接OM,作CF⊥AB于F,
∵DE=6,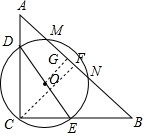
∴OC=3,只有C、O、G三点在一条直线上OG最小,
OM=3,
∴只有OG最小,GM才能最大,从而MN有最大值,
∴G和F重合时,MN有最大值,
∵∠C=90°,BC=6,AC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∵$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CF,
∴CF=4.8,
∴OG=4.8-3=$\frac{9}{5}$,
∴MG=$\frac{12}{5}$,
则MN═2MG=4.8,
故选:B.
点评 本题考查了垂线段最短,垂径定理,勾股定理,过O作OE垂于E,得出C、O、E三点在一条直线上OE最小是解题的关键.


科目:初中数学 来源: 题型:选择题
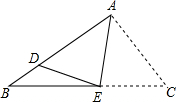 如图,△ABC中,∠ABC=30°,∠ACB=50°,折叠△ACB使点C与AB边上的点D重合,折痕为AE,连DE,则∠AED为( )
如图,△ABC中,∠ABC=30°,∠ACB=50°,折叠△ACB使点C与AB边上的点D重合,折痕为AE,连DE,则∠AED为( )| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,3) | B. | (2,-1) | C. | (0,-1) | D. | (0,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查“神州十一号飞船”各部分零件情况 | |
| B. | 调查旅客随身携带的违禁物品 | |
| C. | 调查全国高中学生对“数学核心素养”的了解 | |
| D. | 调查某校九年级(1)班学生中考体育成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
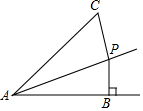 如图,点P是∠BAC的平分线上一点,PB⊥AB于B,且PB=5cm,AC=12,则△APC的面积是( )
如图,点P是∠BAC的平分线上一点,PB⊥AB于B,且PB=5cm,AC=12,则△APC的面积是( )| A. | 30cm2 | B. | 40cm2 | C. | 50cm2 | D. | 60cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
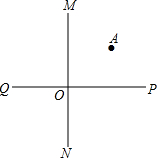 如图所示,直线MN⊥PQ,垂足是点O,点A是∠POM内部的任意一点.
如图所示,直线MN⊥PQ,垂足是点O,点A是∠POM内部的任意一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com