
【题目】已知,如图,在△ABC中,AB=AC,∠ABC=∠ACB,D是AB的中点,DE⊥AB交AC于E,若∠BEC=∠C.

(1)若BE平分∠ABC,求∠A的度数;
(2)若△ABC的周长为10,△BCE的周长为6,求BC的长度。
【答案】(1)36°;(2)2.
【解析】
(1)设∠A的度数为x,根据等腰三角形的性质和线段垂直平分线的性质用x表示出∠ABC和∠C,根据三角形内角和定理列出算式求出x的值即可;
(2)根据线段垂直平分线的性质和三角形周长公式计算即可.
(1)设∠A的度数为x,
∵D是AB的中点,DE⊥AB,
∴EA=EB,
∴∠ABE=∠A=x,
∵BE平分∠ABC,
∴∠ABE=∠CBE=x,
∵∠BEC=∠ABE+∠A=2x,
∴∠C=2x,
∴x+2x+2x=180°,
∴∠A=x=36°;
(2)∵△ABC的周长为10,
∴AB+AC+BC=10,
∵△BCE的周长为6,
∴BE+EC+BC=6,即AC+BC=6,
∴AB=4,
则BC=2.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在学校的社会实践活动中,一批学生协助搬运初一、二两个年级的图书,初一年级需要搬运的图书数量是初二年级需要搬运的图书数量的两倍.上午全部学生在初一年级搬运,下午一半的学生仍然留在初一年级(上下午的搬运时间相等)搬运,到放学时刚好把初一年级的图书搬运完.下午另一半的学生去初二年级搬运图书,到放学时还剩下一小部分未搬运,最后由三个学生再用一整天的时间刚好搬运完.如果这批学生每人每天搬运的效率是相同的,则这批学生共有人数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() ,对角线
,对角线![]() 的中点为
的中点为![]() ,点
,点![]() 同时是正方形
同时是正方形![]() 的一个顶点,
的一个顶点,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,若这两个正方形的边长都是3,将正方形
,若这两个正方形的边长都是3,将正方形![]() 绕点
绕点![]() 转动.
转动.

(1)两个正方形重叠部分的面积________改变(填“会”或“不会”)
(2)两个正方形重叠部分的面积若改变,说明理由;若不改变,直接写出重叠部分的面积.请将答案写在横线上________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根的判别式内容:
△=b2﹣4ac>0一元二次方程_____;
△=b2﹣4ac=0一元二次方程_____;
此时方程的两个根为x1=x2=_____.
△=b2﹣4ac<0一元二次方程_____.
△=b2﹣4ac≥0一元二次方程_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小文同学统计了某小区部分居民每周使用共享单车的时间,并绘制了统计图,如图所示.下面有四个推断:
①小文此次一共调查了![]() 位小区居民
位小区居民
②每周使用时间不足![]() 分钟的人数多于
分钟的人数多于![]() 分钟的人数
分钟的人数
③每周使用时间超过![]() 分钟的人数超过调查总人数的一半
分钟的人数超过调查总人数的一半
④每周使用时间在![]() 分钟的人数最多
分钟的人数最多
根据图中信息,上述说法中正确的是( )

A.①④B.①③C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
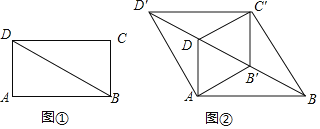
【题目】如图![]() ,BD是矩形ABCD的对角线,
,BD是矩形ABCD的对角线,![]() ,
,![]() 将
将![]() 沿射线BD方向平移到
沿射线BD方向平移到![]() 的位置,使
的位置,使![]() 为BD中点,连接
为BD中点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() .
.
![]() 求证:四边形
求证:四边形![]() 是菱形;
是菱形;
![]() 四边形
四边形![]() 的周长为______;
的周长为______;
![]() 将四边形
将四边形![]() 沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 是直线
是直线![]() 上一个动点(点
上一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,在线段
,在线段![]() 的延长线上取一点
的延长线上取一点![]() ,使得
,使得![]() .过点
.过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .
.

(1)如图1,当点![]() 在线段
在线段![]() 上时,若
上时,若![]() ,则
,则![]() _________;
_________;
(2)当点![]() 在线段
在线段![]() 的延长线上时,在图2中依题意补全图形,并判断
的延长线上时,在图2中依题意补全图形,并判断![]() 与
与![]() 有怎样的数量关系,写出你的结论,并证明;
有怎样的数量关系,写出你的结论,并证明;
(3)在点![]() 运动的过程中,直接写出
运动的过程中,直接写出![]() 与
与![]() 的数量关系为_________.
的数量关系为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
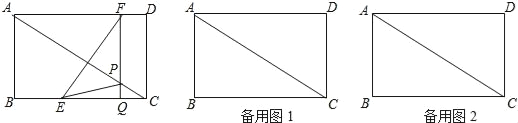
【题目】如图,在矩形ABCD中,AB=6cm,BC=8cm,如果点E由点B出发沿BC方向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为每秒2cm和1cm,FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t秒(0<t<4).
(1)连接EF,若运动时间t= 时,EF⊥AC;
(2)连接EP,当△EPC的面积为3cm2时,求t的值;
(3)若△EQP∽△ADC,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com