
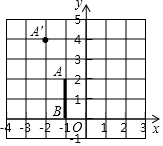
 如图,在平面直角坐标系xOy中,以原点为位似中心,线段AB与线段A′B′是位似图形,若A(-1,2),B(-1,0),A′(-2,4),则B′的坐标为(-2,0).
如图,在平面直角坐标系xOy中,以原点为位似中心,线段AB与线段A′B′是位似图形,若A(-1,2),B(-1,0),A′(-2,4),则B′的坐标为(-2,0).  尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:选择题

| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A是双曲线y=$\frac{6}{x}$在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为底作等腰△ABC,使∠C=120°,且点C在第四象限内,且随着点A的运动,点C的位置也不断变化.但点C始终也在不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值是( )
如图,点A是双曲线y=$\frac{6}{x}$在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为底作等腰△ABC,使∠C=120°,且点C在第四象限内,且随着点A的运动,点C的位置也不断变化.但点C始终也在不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值是( )| A. | -1 | B. | -2 | C. | -2$\sqrt{3}$ | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
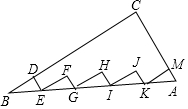 如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为24.
如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为24.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a-b+c<0;⑤3a+c>0.其中正确结论的序号是①④⑤.
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a-b+c<0;⑤3a+c>0.其中正确结论的序号是①④⑤.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 280x+230x=400 | B. | 280x+230x=400×2 | C. | 280x-230x=400 | D. | 280x-230x=400×2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com