
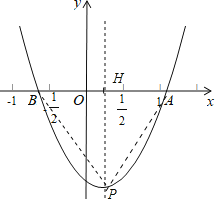
【题目】如图,抛物线![]() (a,b,c是常数,
(a,b,c是常数,![]() )与x轴交于A,B两点,顶点
)与x轴交于A,B两点,顶点![]() .给出下列结论:①
.给出下列结论:①![]() ;②若
;②若![]() ,
,![]() ,
,![]() 在抛物线上,则
在抛物线上,则![]() ;③关于x的方程
;③关于x的方程![]() 有实数解,则
有实数解,则![]() ;④当
;④当![]() 时,
时,![]() 为等腰直角三角形.其中正确结论是________(填写序号).
为等腰直角三角形.其中正确结论是________(填写序号).

【答案】①②④
【解析】
利用二次函数的性质一一判断即可.
∵-![]() <
<![]() ,a>0,
,a>0,
∴a>-b,
∵x=-1时,y>0,
∴a-b+c>0,
∴2a+c>a-b+c>0,故①正确,
若![]() ,
,![]() ,
,![]() 在抛物线上,
在抛物线上,
由图象法可知,y1>y2>y3;故②正确,
∵抛物线与直线y=t有交点时,方程ax2+bx+c=t有解,t≥n,
∴ax2+bx+c-t=0有实数解
要使得ax2+bx+k=0有实数解,则k=c-t≤c-n;故③错误,
设抛物线的对称轴交x轴于H.
∵![]() ,
,
∴b2-4ac=4,
∴x=![]() ,
,
∴|x1-x2|=![]() ,
,
∴AB=2PH,
∵BH=AH,
∴PH=BH=AH,
∴△PAB是直角三角形,
∵PA=PB,
∴△PAB是等腰直角三角形.故④正确.
故答案为①②④.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
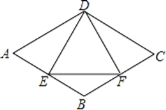
A.3
B.4
C.1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧,与y轴交于点C,点A、点B的横坐标是一元二次方程x2﹣4x﹣12=0的两个根.
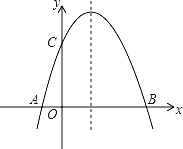
(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图,在二次函数对称轴上是否存在点P,使△APC的周长最小?若存在,请求出点P的坐标;若不存在,那个说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应市委,市政府提出的“实现伟大中国梦,建设美丽攀枝花”的号召,我市某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
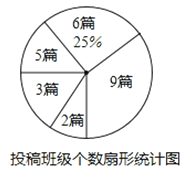
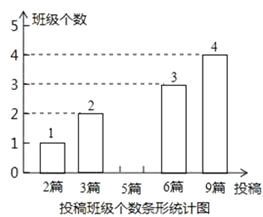
(1)求扇形统计图中投稿篇数为2所对应的扇形的圆心角的度数:
(2)求该校八,九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数为9篇的两个班级中,八,九年级各有两个班,校学生会准备从这四个中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A、B两点,点A的坐标是(﹣2,1),点B的坐标是(1,n);
的图象交于A、B两点,点A的坐标是(﹣2,1),点B的坐标是(1,n);
(1)分别求一次函数与反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式kx+b≥![]() 的解集.
的解集.
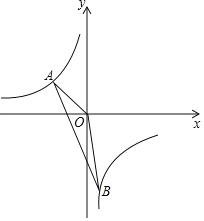
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,与x轴相交于点B.
,与x轴相交于点B.
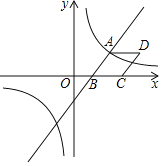
(1)求k的值;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数![]() 的图象,请直接写出:当
的图象,请直接写出:当![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程
有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程![]() 的两个根是2和4,则方程
的两个根是2和4,则方程![]() 就是“倍根方程”.
就是“倍根方程”.
(1)若一元二次方程![]() 是“倍根方程”,则c ;
是“倍根方程”,则c ;
(2)若![]() 是“倍根方程”,求代数式
是“倍根方程”,求代数式![]() 的值;
的值;
(3)若方程![]() 是倍根方程,且不同的两点M(k+1,5),N(3-k,5)都在抛物线
是倍根方程,且不同的两点M(k+1,5),N(3-k,5)都在抛物线![]() 上,求一元二次方程
上,求一元二次方程![]() 的根.
的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 以每秒3个单位长的速度运动至点
以每秒3个单位长的速度运动至点![]() ,过点
,过点![]() 作
作![]() 射线
射线![]() 于点
于点![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒(
秒(![]() ).
).
(1)线段![]() 的长为 (用含
的长为 (用含![]() 的代数式表示)
的代数式表示)
(2)当![]() 与
与![]() 的周长的比为
的周长的比为![]() 时,求
时,求![]() 的值.
的值.
(3)设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当直线![]() 把
把![]() 分成的两部分图形中有一个是轴对称图形时,直接写出
分成的两部分图形中有一个是轴对称图形时,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com