
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.
(1)求证:直线BF是⊙O的切线.
(2)若CD=2![]() ,OP=1,求线段BF的长.
,OP=1,求线段BF的长.

科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(b,-2a).且![]() +|b-l|=0.CD∥AB,AD∥BC
+|b-l|=0.CD∥AB,AD∥BC
(1)直接写出B、C、D各点的坐标:B 、C 、D ;
(2)如图1,P(3,10),点E,M在四边形ABCD的边上,且E在第二象限.若△PEM是以PE为直角边的等腰直角三角形,请直接写出点E的坐标,并对其中一种情况计算说明;
(3)如图2,F为y轴正半轴上一动点,过F的直线j∥x轴,BH平分∠FBA交直线j于点H.G为BF上的点,且∠HGF=∠FAB,F在运动中FG的长度是否发生变化?若变化,求出变化范围;若不变,求出定值.

查看答案和解析>>
科目:初中数学 来源: 题型:
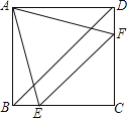
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②BD=1+![]() ;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )

A.AB=CDB.AB∥CDC.∠A=∠CD.BC=AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证:
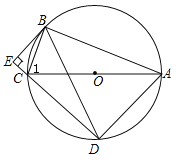
(1)∠1=∠BAD;
(2)BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分):78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93,整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) | 频数 |
| 5 |
|
|
| 11 |
|
|
| 2 |
回答下列问题:
(1)以上30个数据中,中位数是_____;频数分布表中![]() ____;
____;![]() _____;
_____;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com