
一次函数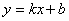 与坐标轴相交于A,B两点(A在x轴上),与反比例函数
与坐标轴相交于A,B两点(A在x轴上),与反比例函数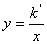 的图象相交于C点,且AO=2BO,点C坐标为(-1,4).
的图象相交于C点,且AO=2BO,点C坐标为(-1,4).
(1)试确定一次函数与反比例函数的解析式;
(2)求不等式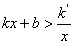 的解;
的解;
(3)在解答本题过程中,你发现用到了哪些数学思想方法,请简单地写出.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
观察与思考:阅读下列材料,并解决后面的问题.
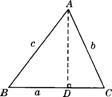 在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作
AD⊥BC于D(如图),则sinB= ,sinC=
,sinC= ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即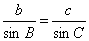 .同理有:
.同理有: ,
, ,
,
所以
即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.
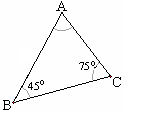
(1)如图,△ABC中,∠B=450,∠C=750,BC=60,则∠A= ;AC= ;
(2)如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB及灯塔A距C处的距离。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(4,4),反比例函数的图象经过CB的中点D,若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S=4时,x的值为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
关于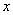 的方程
的方程 有两个不相等的实数根,且较小的根为2,则下列结论:①
有两个不相等的实数根,且较小的根为2,则下列结论:①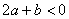 ;②
;②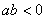 ;③关于
;③关于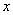 的方程
的方程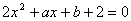 有两个不相等的实数根;④抛物线
有两个不相等的实数根;④抛物线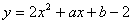 的顶点在第四象限。其中正确的结论有( )
的顶点在第四象限。其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
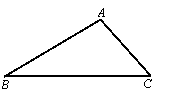
如图,在△ABC中,∠BAC = 2∠C.
(1)在图中作出△ABC的内角平分线AD.(要求:尺规作图,
保留作图痕迹,不写证明)
(2)在已作出的图形中,直接写出一对相似三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
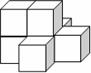
右图是一个由7个同样的立方体叠成的几何体,则这一几何体的三 视图中,既是轴对称图形又是中心对称图形的是( )
A.主视图 B. 左视图
C.俯视图 D. 左视图与俯视图
查看答案和解析>>
科目:初中数学 来源: 题型:
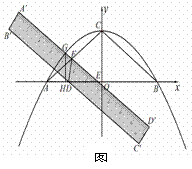
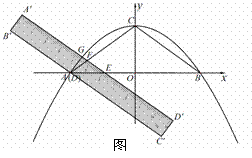
抛物线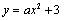 交
交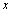 轴于A、B,交
轴于A、B,交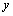 轴于C.将一把直尺如图放置在直角坐标系中,使直尺边
轴于C.将一把直尺如图放置在直角坐标系中,使直尺边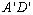 ∥
∥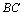 ,直尺边
,直尺边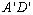 交
交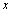 轴于E,交AC于F,交抛物线于G,直尺另一边
轴于E,交AC于F,交抛物线于G,直尺另一边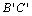 交
交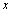 轴于D.当点D与点A重合时,把直尺沿
轴于D.当点D与点A重合时,把直尺沿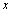 轴向右平移,当点E与点B重合时,停止平移,在平移过程中,△FDE的面积与直尺平移距离的函数图象如图(3)所示.
轴向右平移,当点E与点B重合时,停止平移,在平移过程中,△FDE的面积与直尺平移距离的函数图象如图(3)所示.
(1)请你求出DE的长及抛物线解析式;
(2)在直尺平移过程中,直尺边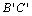 上是否存在一点P,使点
上是否存在一点P,使点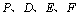 构成的四边形这菱形,若存在,请你求出点P坐标;若不存在,请说明理由;
构成的四边形这菱形,若存在,请你求出点P坐标;若不存在,请说明理由;
(3)过G作GH⊥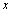 轴于H
轴于H
① 在直尺平移过程中,请你求出GH+HO的最大值;
②点Q、R分别是HC、HB的中点,请你直接写出在直尺平移过程中,线段QR扫过的图形的面积和周长.
(主要考查学生一次函数、二次函数、菱形、相似三角形等知识的综合运用,考试难度C)
 | |||
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com