
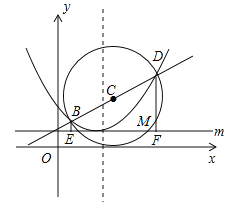
【题目】如图,已知抛物线![]() (a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线
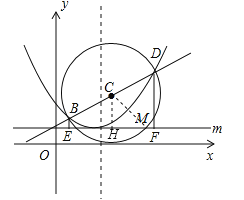
(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线![]() 与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
(1)求抛物线的解析式;
(2)证明:圆C与x轴相切;
(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求MF的值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)可设抛物线的顶点式,再结合抛物线过点(4,2),可求得抛物线的解析式;
(2)联立直线和抛物线解析式可求得B、D两点的坐标,则可求得C点坐标和线段BD的长,可求得圆的半径,可证得结论;
(3)过点C作CH⊥m于点H,连接CM,可求得MH,利用(2)中所求B、D的坐标可求得FH,则可求得MF和BE的长,可求得其比值.
试题解析:
(1)∵已知抛物线![]() (a≠0)的图象的顶点坐标是(2,1),∴可设抛物线解析式为
(a≠0)的图象的顶点坐标是(2,1),∴可设抛物线解析式为![]() ,∵抛物线经过点(4,2),∴
,∵抛物线经过点(4,2),∴![]() ,解得a=
,解得a=![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ,即
,即![]() ;
;
(2)联立直线和抛物线解析式可得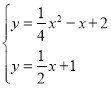 ,解得:
,解得: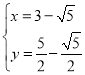 或
或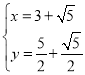 ,∴B(
,∴B(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),∵C为BD的中点,∴点C的纵坐标为
),∵C为BD的中点,∴点C的纵坐标为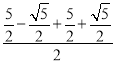 =
=![]() ,∵BD=
,∵BD=![]() =5,∴圆的半径为
=5,∴圆的半径为![]() ,∴点C到x轴的距离等于圆的半径,∴圆C与x轴相切;
,∴点C到x轴的距离等于圆的半径,∴圆C与x轴相切;
(3)如图,过点C作CH⊥m,垂足为H,连接CM,由(2)可知CM=![]() ,CH=
,CH=![]() ﹣1=
﹣1=![]() ,在Rt△CMH中,由勾股定理可求得MH=2,∵HF=
,在Rt△CMH中,由勾股定理可求得MH=2,∵HF=![]() =
=![]() ,∴MF=HF﹣MH=
,∴MF=HF﹣MH=![]() ,∵BE=
,∵BE=![]() ﹣1=
﹣1=![]() ,∴
,∴![]() =
=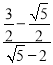 =
=![]() .
.


科目:初中数学 来源: 题型:
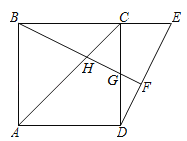
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交BC于G.
(1)求证:BG=DE;
(2)若点G为CD的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
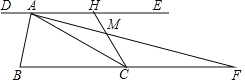
【题目】如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM=![]() AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是
AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是![]() ,则
,则![]() 的值是 .
的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大报告指出:“建设生态文明,是关系人民福祉、关乎民族未来的长远大计”,这些年党和政府在生态文明的发展进程上持续推进,在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国际社会广泛赞誉.将1 460 000 000用科学记数法表示为( )
A.146×107
B.1.46×107
C.1.46×109
D.1.46×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
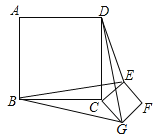
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③![]() ,其中正确结论是 (填序号)
,其中正确结论是 (填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com