
 如图,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则彩带最短要用10m.
如图,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则彩带最短要用10m.  名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,若$\frac{3}{2}$∠BOD=∠DOE.
如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,若$\frac{3}{2}$∠BOD=∠DOE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
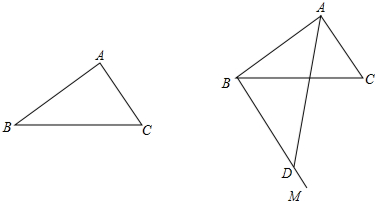
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
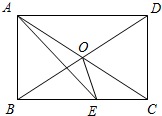 如图,矩形ABCD中,对角线AC、BD交于点O,在BC上取BE=BO,连结AE,且∠BOE=75°.
如图,矩形ABCD中,对角线AC、BD交于点O,在BC上取BE=BO,连结AE,且∠BOE=75°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com