
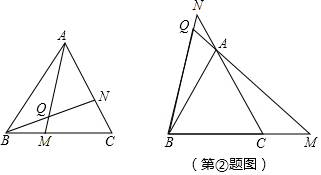
���� ��1����֤����ABM�ա�BCN������á�BAM=��CBN������������ǵ����ʿ�֤��BQM=60�㣻
��2�����ɡ�BQM=60�����á�BAM=��CBN����֤����ABM�ա�BCN�������BM=CN������������֤����ABM�ա�BCN��ͬ��1������á�BQM=60�㣮
��� ��1��֤����
�ߡ�ABCΪ�ȱ������Σ�
��AB=BC����ABC=��C=60�㣬
�ڡ�ABM�͡�BCN��
$\left\{\begin{array}{l}{AB=BC}\\{��ABM=��C}\\{BM=CN}\end{array}\right.$
���ABM�ա�BCN��SAS����
���BAM=��CBN��
���BQM=��BAM+��ABQ=��CBN+��ABQ=��ABM=60�㣻
��2���⣺
���ǣ�֤�����£�
�ߡ�BQM=60�㣬
���ABM=��BQM��
���BAM+��ABQ=��CBN+��ABQ��
���BAM=��CBN��
�ڡ�ABM�͡�BCN��
$\left\{\begin{array}{l}{��BAM=��CBN}\\{AB=BC}\\{��ABM=��C}\end{array}\right.$
���ABM�ա�BCN��ASA����
��BM=CN��
���ǣ�֤������ͬ��1����
�ʴ�Ϊ���ǣ��ǣ�
���� ������Ҫ����ȫ�������ε��ж������ʣ�����ȫ�������ε��ж���������SSS��SAS��ASA��AAS��HL����ȫ�������ε����ʣ�����Ӧ����ȡ���Ӧ����ȣ��ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�AB=AC������ABC�Ƶ�A����ʱ�뷽����ת100�㣬�õ���ADE������BD��CE��
��ͼ����ABC�У�AB=AC������ABC�Ƶ�A����ʱ�뷽����ת100�㣬�õ���ADE������BD��CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
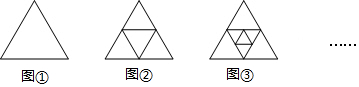
| A�� | 14 | B�� | 15 | C�� | 16 | D�� | 17 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ס�������ͬ����ͼ��ʾ�ĵ��³���ȵ��ݣ����˵�1��4�������һ������ݣ�
�ס�������ͬ����ͼ��ʾ�ĵ��³���ȵ��ݣ����˵�1��4�������һ������ݣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
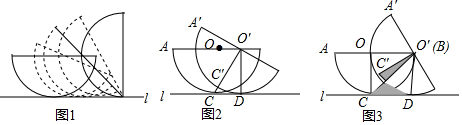 ��ͼ1��һ���뾶Ϊ2�İ�Բ��ƽ��������˳ʱ�����������ƽ�濴��ֱ��l����ʼλ�õİ�ԲO��ֱ��l�����ڵ�C��AB��l�����������У���ԲO����ֱ��l�����ڵ�D����A��B��C�ڰ�ԲO���ϵĶ�Ӧ��ֱ�ΪA�䡢B�䡢C�䣮
��ͼ1��һ���뾶Ϊ2�İ�Բ��ƽ��������˳ʱ�����������ƽ�濴��ֱ��l����ʼλ�õİ�ԲO��ֱ��l�����ڵ�C��AB��l�����������У���ԲO����ֱ��l�����ڵ�D����A��B��C�ڰ�ԲO���ϵĶ�Ӧ��ֱ�ΪA�䡢B�䡢C�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵxOy�У�����������y=2x�뷴��������y=$\frac{k}{x}$��ͼ����A��B���㣬A��ĺ�����Ϊ2��AC��x���ڵ�C������BC��
��ͼ����ƽ��ֱ������ϵxOy�У�����������y=2x�뷴��������y=$\frac{k}{x}$��ͼ����A��B���㣬A��ĺ�����Ϊ2��AC��x���ڵ�C������BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
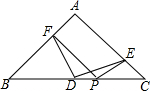 ��ͼ��Rt��ABC�У���BAC=90�㣬AB=AC��DΪBC���е㣬PΪBC��һ�㣬PF��AB��F��PE��AC��E����DF��DE�Ĺ�ϵΪDF=DE��DF��ED��
��ͼ��Rt��ABC�У���BAC=90�㣬AB=AC��DΪBC���е㣬PΪBC��һ�㣬PF��AB��F��PE��AC��E����DF��DE�Ĺ�ϵΪDF=DE��DF��ED���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com