
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现 如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
② 线段DE与AC的位置关系是;
②设△BDC的面积为S1 , △AEC的面积为S2 , 则S1与S2的数量关系是 . 
(2)猜想论证 当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
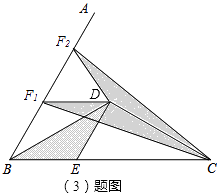
(3)拓展探究 已知∠ABC=60°,点D是角平分线上一点,BD=CD=4,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S△DCF=S△BDE , 请直接写出相应的BF的长.
【答案】
(1)DE∥AC;S1=S2
(2)解:如图,∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,
∴∠ACN=∠DCM,
∵在△ACN和△DCM中,
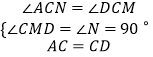 ,
,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
(3)解:如图,过点D作DF1∥BE,易求四边形BEDF1是菱形,
所以BE=DF1,且BE、DF1上的高相等,
此时S△DCF1=S△BDE;
过点D作DF2⊥BD,
∵∠ABC=60°,F1D∥BE,
∴∠F2F1D=∠ABC=60°,
∵BF1=DF1,∠F1BD= ![]() ∠ABC=30°,∠F2DB=90°,
∠ABC=30°,∠F2DB=90°,
∴∠F1DF2=∠ABC=60°,
∴△DF1F2是等边三角形,
∴DF1=DF2,
∵BD=CD,∠ABC=60°,点D是角平分线上一点,
∴∠DBC=∠DCB= ![]() ×60°=30°,
×60°=30°,
∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°,
∠CDF2=360°﹣150°﹣60°=150°,
∴∠CDF1=∠CDF2,
∵在△CDF1和△CDF2中,
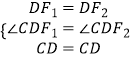 ,
,
∴△CDF1≌△CDF2(SAS),
∴点F2也是所求的点,
∵∠ABC=60°,点D是角平分线上一点,DE∥AB,
∴∠DBC=∠BDE=∠ABD= ![]() ×60°=30°,
×60°=30°,
又∵BD=4,
∴BE= ![]() ×4÷cos30°=2÷
×4÷cos30°=2÷ ![]() =
= ![]() ,
,
∴BF1= ![]() ,BF2=BF1+F1F2=
,BF2=BF1+F1F2= ![]() +
+ ![]() =
= ![]() ,
,
故BF的长为 ![]() 或
或 ![]() .
.
【解析】解:(1)①∵△DEC绕点C旋转点D恰好落在AB边上, ∴AC=CD,
∵∠BAC=90°﹣∠B=90°﹣30°=60°,
∴△ACD是等边三角形,
∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,
∴DE∥AC;
②∵∠B=30°,∠C=90°,
∴CD=AC= ![]() AB,
AB,
∴BD=AD=AC,
根据等边三角形的性质,△ACD的边AC、AD上的高相等,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
所以答案是:DE∥AC;S1=S2;


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x 度时,应交电费为y 元.具体收费情况如折线图所示,请根据图象回答下列问题:
(1)“基础电价”是____________元 ![]() 度;
度;
(2)求出当x>240 时,y与x的函数表达式;
(3)若紫豪家六月份缴纳电费132元,求紫豪家这个月用电量为多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点![]() 点P第1次向上跳动1个单位至点
点P第1次向上跳动1个单位至点![]() ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点![]() ,第3次向上跳动1个单位至点
,第3次向上跳动1个单位至点![]() ,第4次向右跳动3个单位至点
,第4次向右跳动3个单位至点![]() ,第5次又向上跳动1个单位至点
,第5次又向上跳动1个单位至点![]() ,第6次向左跳动4个单位至点
,第6次向左跳动4个单位至点![]() ,
,![]() 照此规律,点P第100次跳动至点
照此规律,点P第100次跳动至点![]() 的坐标是
的坐标是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y= ![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是OC边上一点,且△FBC∽△DEB,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB=40cm.
(1)如图①,点P沿线段AB自点A向点B以3厘米/秒运动,同时点Q线段BA自B点向点A以5厘米/秒运动,问经过几秒后P、Q相遇?
(2)几秒钟后,P、Q相距16厘米?
(3)如图②,AO=PO=8厘米,∠POB=40°,点P绕点O以20度/秒的速度顺时针旋转一周停止,同时点Q沿直线BA自B点向点A运动,假若P、Q两点能相遇,求Q运动的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
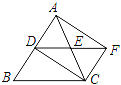
【题目】如图,在△BC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.若使四边形ADCF是正方形,则应在△ABC中再添加一个条件为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值
(1)2x-{-3y+[3x-2(3x-y)]},其中x=-1,y=![]() .
.
(2)5(3a2b-ab2-1)-(ab2+3a2b-5),其中a=![]() ,b=
,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,收费标准如下:
人数m | 0<m≤100 | 100<m≤200 | m>200 |
收费标准(元/人) | 90 | 85 | 75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20 800元,若两校联合组团只需花费18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗?为什么?
(2)两所学校报名参加旅游的学生各有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com