

 或
或 ;(2)当a=2时,b=2,2S1S3-S22有最大值是16.
;(2)当a=2时,b=2,2S1S3-S22有最大值是16. PB=2,当PA=PD、PD=DA时,△PAD是等腰三角形,作辅助线DO
PB=2,当PA=PD、PD=DA时,△PAD是等腰三角形,作辅助线DO AP交PA于G,然后由正方形的性质、勾股定理易知△PAD△DGA,从而用对应边的相似比可得.
AP交PA于G,然后由正方形的性质、勾股定理易知△PAD△DGA,从而用对应边的相似比可得.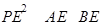 得到关系式,从而利用二次函数最大值概念求得.
得到关系式,从而利用二次函数最大值概念求得. AB=2,
AB=2,



 ,AP=
,AP=
 或
或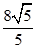 时,△PAD是等腰三角形.
时,△PAD是等腰三角形.
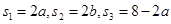
 ,即
,即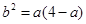



 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.外切 | B.相交 | C.内切 | D.内含 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com