
分析 假设电线杆AB落在墙上的影子CD的高为x米,如果没有墙CD,则影子落在点E,利用在同一时刻物高与影长的比相等首先求出DE=$\frac{1}{2}$x米,再根据AB:BE=CD:DE,得到8:(3+$\frac{1}{2}$x)=1:0.5,解方程即可.
解答  解:如图:假设电线杆AB落在墙上的影子CD的高为x米,如果没有墙CD,则影子落在点E,
解:如图:假设电线杆AB落在墙上的影子CD的高为x米,如果没有墙CD,则影子落在点E,
∵在同一时刻物高与影长的比相等,
∴CD:DE=1:0.5,
∴DE=$\frac{1}{2}$x米,
∵AB:BE=CD:DE,
∴8:(3+$\frac{1}{2}$x)=1:0.5,
∴x=2,
故电线杆的影子落在墙上的影长是2米.
点评 本题考查了相似三角形的应用,解题的关键是知道在同一时刻同一地点任何物体的高与其影子长的比值相同这个结论.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
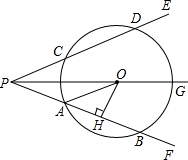 如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,过O作OH⊥AB于点H,已知PH=2OH,OA∥PE.
如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,过O作OH⊥AB于点H,已知PH=2OH,OA∥PE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com