Question

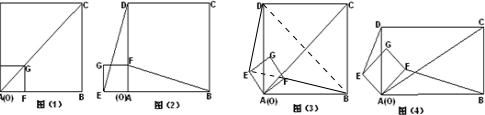
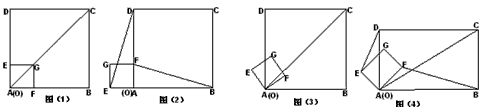
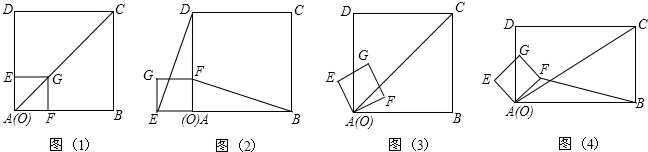
25、把正方形OFGE纸板按如图①方式放置在正方形纸板ABCD上，顶点G在对角线AC，并把正方形OFGE绕顶点A沿逆时针方向旋转，旋转角为а．
（1）如图②，当а=90°时，请直接写出线段DE与BF的数量关系和位置关系；
（2）如图③，当0°＜а＜90°时，（1）中的结论是否发生改变？若不变，请给出证明．若发生改变，请举例说明；
（3）如图④，将图①、图③中的两个正方形都改为矩形，其他条件不变，设AB=kAD（k＞0），当0°＜а＜90°时，（1）中的结论是否发生改变？若不变，请给出证明．若发生改变，请写出改变后的新结论，并给出证明．

Answer 1

分析：（1）此题可通过全等三角形来求解；首先证△AED≌△AFB，然后根据全等三角形得到的等角和等边来进行判断．
（2）思路同（1），依然是根据△AED≌△AFB来得到所求的结论．
（3）此题要通过相似三角形来解，首先根据已知条件，易证得AE、AF与AD、AB对应成比例，而∠DAE=∠FAB，即可证得△AED∽△AFB，由此得DE、BF的比例关系，在求它们的位置关系时，可参照（2）的解法．

解答：解：（1）DE=BF，DE⊥BF；理由如下：
∵四边形AFGE、四边形ABCD都是正方形，
∴AE=AF，AD=AB，∠DAE=∠BAF=90°，
∴△AED≌△AFB，得DE=BF，∠DEA=∠AFB；
由于∠ABF、∠AFB互余，因此∠ABF、∠DEA互余，即∠DEA+∠ABF=90°，故DE⊥BF；
因此DE、BF的数量关系为相等，位置关系为垂直．

（2）不改变；
证明：如图（3），连接DE，BF，BD；
同（1）可得：AE=AF，AD=AB，∠DAE=∠BAF（旋转角），
∴△AED≌△AFB，得DE=BF，∠EDA=∠FBA；
由于∠EDA+∠ADB+∠DBF=∠ABF+∠ADB+∠DBF=90°，即∠EDB+∠DBF=90°，
故DE⊥BF，所以（1）的结论依然成立．

（3）BF=kDE，DE⊥BF；理由如下：
∵AB：AD=AF：AE=k，且∠DAE=∠BAF，
∴△ADE∽△ABF，且相似比为1：k，
故BF=kDE，∠EDA=∠FBA；
同（2）可证得DE⊥BF；
故BF、DE的数量关系为：BF=kDE，位置关系为：垂直．

点评：此题主要考查的是全等三角形及相似三角形的判定和性质，还涉及到正方形、矩形的性质，考查了学生对知识的综合应用能力．