
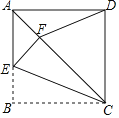
【题目】如图,在正方形ABCD的边AB上取一点E,连接CE,将△BCE沿CE翻折,点B恰好与对角线AC上的点F重合,连接DF,若BE=1,则△CDF的面积是_____.
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
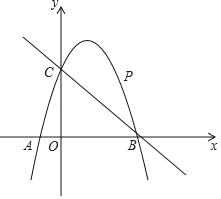
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
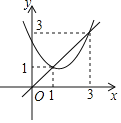
【题目】如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>![]() 时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
A. ①②④B. ②③④C. ②④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣ | 3 |
| 3 |
下列结论:
(1)abc<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)16a+4b+c<0;
(4)抛物线与坐标轴有两个交点;
(5)x=3是方程ax2+(b﹣1)x+c=0的一个根;
其中正确的个数为( )
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
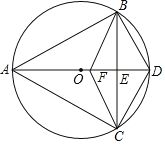
(1)求证:BE=CE;
(2)若BC=8,AD=10,求四边形BFCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,F为AB边上一点,满足CF⊥CP,过点B作BM⊥CF,分别交AC、CF于点M、N
(1)若AC=![]() AP,AC=4
AP,AC=4![]() ,求△ACP的面积;
,求△ACP的面积;
(2)若BC=MC,证明:CP﹣BM=2FN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是数值转换机的示意图,小明按照其对应关系画出了y与x的函数图象(如图):
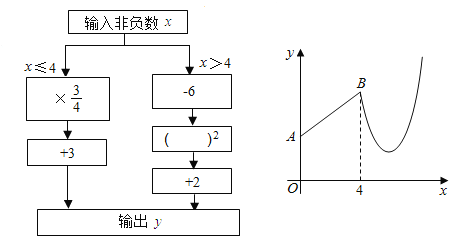
(1)分别写出当0≤x≤4与x>4时,y与x的函数关系式:
(2)求出所输出的y的值中最小一个数值;
(3)写出当x满足什么范围时,输出的y的值满足3≤y≤6.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,直径AD交BC于点E,延长AD至点F,使DF=2OD,连接FC并延长交过点A的切线于点G,且满足AG∥BC,连接OC,若cos∠BAC=![]() ,BC=6.
,BC=6.

(1)求证:∠COD=∠BAC;
(2)求⊙O的半径OC;
(3)求证:CF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为![]() ,中轴轴心
,中轴轴心![]() 到地面的距离
到地面的距离![]() 为
为![]() ,后轮中心
,后轮中心![]() 与中轴轴心
与中轴轴心![]() 连线与车架中立管
连线与车架中立管![]() 所成夹角
所成夹角![]() ,后轮切地面
,后轮切地面![]() 于点
于点![]() .为了使得车座
.为了使得车座![]() 到地面的距离
到地面的距离![]() 为
为![]() ,应当将车架中立管
,应当将车架中立管![]() 的长设置为_____________
的长设置为_____________![]() .
.
(参考数据: ![]()
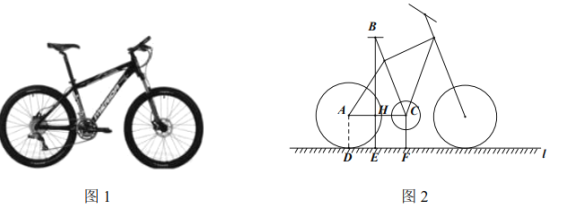
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com