
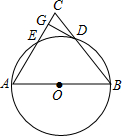
 如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于D,交AC于F,DG⊥AC于G.
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于D,交AC于F,DG⊥AC于G.分析 (1)连接AD,OD,由AB为⊙O的直径,得到AD⊥BC,根据等腰三角形的性质得到∠BAD=∠CAD,∠BAD=∠ADO,等量代换得到∠CAD=∠ADO,根据平行线的判定和性质得到DG⊥OD,于是得到结论;
(2)连接BE,根据垂径定理得到OD⊥BE,BH=EH,根据三角形的中位线的性质得到OH=$\frac{1}{2}$AE=$\frac{7}{2}$,根据勾股定理列方程即可得到结论.
解答 (1)证明:连接AD,OD,
∵AB为⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,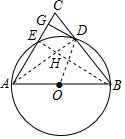
∴AC∥OD,
∵DG⊥AC,
∴DG⊥OD,
∴DG是⊙O的切线;
(2)解:连接BE,
∵∠CAD=∠BAD,
∴$\widehat{DE}$=$\widehat{BD}$,
∴OD⊥BE,BH=EH,
∵AO=OB,
∴OH=$\frac{1}{2}$AE=$\frac{7}{2}$,
∵BC=6,
∴BD=3,
∵BD2-DH2=BH2,OB2-OH2=BH2,
∴32-(OD-$\frac{7}{2}$)2=OD2-($\frac{7}{2}$)2,
∴OD=$\frac{9}{2}$(负值舍去),
∴AB=2OD=9.
点评 本题考查了切线的判定,圆周角定理,角平分线的定义,平行线的性质,勾股定理,等腰三角形的性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
 随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
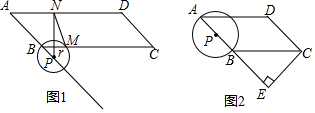
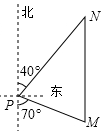 如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )
如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )| A. | 40海里 | B. | 60海里 | C. | 70海里 | D. | 80海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
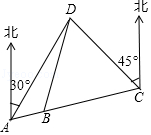 如图,A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.
如图,A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地,货车的路程y1(km),小轿车的路程y2(km)与时间x(h)的对应关系如图所示,下列结论错误的是( )
一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地,货车的路程y1(km),小轿车的路程y2(km)与时间x(h)的对应关系如图所示,下列结论错误的是( )| A. | 甲、乙两地的距离为420km | B. | y1=60x,y2=$\left\{\begin{array}{l}{90x}\\{100x-230}\end{array}\right.$ | ||
| C. | 货车出发4.5h与小轿车首次相遇 | D. | 两车首次相遇时距乙地150km |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com