
| A. | $\frac{1-3x}{2}$-3=2x+3 | B. | $\frac{3(1-3x)}{2}$-3=2x | C. | 3(1-3x)-6=4x | D. | 3(1-3x)-4x=6 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-$\frac{1}{10}$(x-4)2+3,由此可知铅球推出的距离是(4+$\sqrt{30}$)m.
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-$\frac{1}{10}$(x-4)2+3,由此可知铅球推出的距离是(4+$\sqrt{30}$)m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠ACD是△ABC的一个外角,过点D作直线,分别交AC和AB于点E,H.下列的结论中一定不正确的是( )
如图,∠ACD是△ABC的一个外角,过点D作直线,分别交AC和AB于点E,H.下列的结论中一定不正确的是( )| A. | ∠B>∠ACD | B. | ∠B+∠ACB=180°-∠A | C. | ∠B+∠ACB<180° | D. | ∠HEC>∠B |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
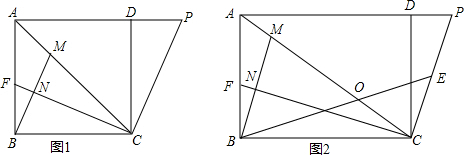
 如图,正方形ABCD中,E为AB上一点,F是BC延长线上一点,且AE=CF,M是EF的中点.
如图,正方形ABCD中,E为AB上一点,F是BC延长线上一点,且AE=CF,M是EF的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
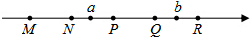 如图,M,N,P,Q,R分别是数轴上五个整数所对应的点,其中有一点是原点,并且MN=NP=PQ=QR=1.数a对应的点在N与P之间,数b对应的点在Q与R之间,若|a|+|b|=3,则原点可能是( )
如图,M,N,P,Q,R分别是数轴上五个整数所对应的点,其中有一点是原点,并且MN=NP=PQ=QR=1.数a对应的点在N与P之间,数b对应的点在Q与R之间,若|a|+|b|=3,则原点可能是( )| A. | M或Q | B. | P或R | C. | N或R | D. | P或Q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com