
分析 ①移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可;
②去分母,分解因式,即可得出两个一元一次方程,求出方程的解即可;
③先求出b2-4ac的值,再代入公式求出即可;
④设$\frac{x}{{x}^{2}+1}$=y,则原方程化为y+$\frac{1}{y}$=$\frac{5}{2}$,求出方程的解,即可求出答案.
解答 解:①x2-3x-1=0,
x2-3x=1,
x2-3x+($\frac{3}{2}$)2=1+($\frac{3}{2}$)2,
(x-$\frac{3}{2}$)2=$\frac{13}{4}$,
x-$\frac{3}{2}$=±$\frac{\sqrt{13}}{2}$,
x1=$\frac{3+\sqrt{13}}{2}$,x2=$\frac{3-\sqrt{13}}{2}$;
②$\frac{2}{7}$x2+x-$\frac{4}{7}$=0,
2x2+7x-4=0,
(2x-1)(x+4)=0,
2x-1=0,x+4=0,
x1=$\frac{1}{2}$,x2=-4;
③-3x2+4x+5=0,
b2-4ac=42-4×(-3)×5=76,
x=$\frac{-4±\sqrt{76}}{2×(-3)}$,
x1=$\frac{2-\sqrt{19}}{3}$,x2=$\frac{2+\sqrt{19}}{3}$;
④$\frac{x}{{x}^{2}+1}$+$\frac{{x}^{2}+1}{x}$=$\frac{5}{2}$,
设$\frac{x}{{x}^{2}+1}$=y,则原方程化为:y+$\frac{1}{y}$=$\frac{5}{2}$,
即2y2-5y+2=0,
解得:y1=$\frac{1}{2}$,y2=2,
当y=$\frac{1}{2}$时,$\frac{x}{{x}^{2}+1}$=$\frac{1}{2}$,
解得:x1=x2=1,
当y=2时,$\frac{x}{{x}^{2}+1}$=2,
x2-x=2=0,
此方程无解;
经检验x1=x2=1是原方程的解,
所以原方程组的解为:x1=x2=1.
点评 本题考查了解一元二次方程和解分式方程的应用,能选择适当的方法解一元二次方程是解①②③得关键,能正确换元是解④的关键.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:解答题
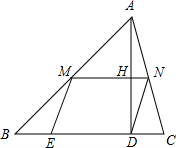 如图,在△ABC中,AD⊥BC,垂足为D,?DEMN的一边DE在BC上,另两个顶点M,N分别在AB,AC上,MN交AD于H.当ND=NC时,求$\frac{AH}{AD}$的值.
如图,在△ABC中,AD⊥BC,垂足为D,?DEMN的一边DE在BC上,另两个顶点M,N分别在AB,AC上,MN交AD于H.当ND=NC时,求$\frac{AH}{AD}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2(2x-1)-1=2-3x | B. | 6(2x+1)+6=3(2-3x) | C. | 6(2x+1)-1=3(2-3x) | D. | 2(2x-1)-6=2-3x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com