
【题目】小明要测量公园北湖水隔开的两棵大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°方向.
(1)求∠ABC的度数;
(2)求两棵大树A和B之间的距离(结果精确到1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.449)
≈2.449)
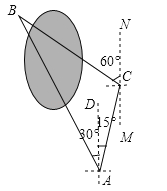
【答案】(1)30°;(2)386.
【解析】
试题分析:(1)先利用平行线的性质得∠ACM=∠DAC=15°,再利用平角的定义计算出∠ACB=105°,然后根据三角形内角和计算∠ABC的度数;
(2)作CH⊥AB于H,如图,易得△ACH为等腰直角三角形,则AH=CH=![]() AC=
AC=![]() ,在Rt△BCH中利用含30度的直角三角形三边的关系得到BH=
,在Rt△BCH中利用含30度的直角三角形三边的关系得到BH=![]() CH=
CH=![]() ,AB=AH+BH=
,AB=AH+BH=![]() ,然后进行近似计算即可.
,然后进行近似计算即可.
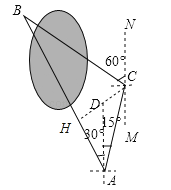
试题解析:(1)∵CM∥AD,∴∠ACM=∠DAC=15°,∴∠ACB=180°﹣∠BCN﹣∠ACM=180°﹣60°﹣15°=105°,而∠BAC=30°+15°=45°,∴∠ABC=180°﹣45°﹣105°=30°;
(2)作CH⊥AB于H,如图,∵∠BAC=45°,∴△ACH为等腰直角三角形,∴AH=CH=![]() AC=
AC=![]() ×200=
×200=![]() ,在Rt△BCH中,∵∠HBC=30°,∴BH=
,在Rt△BCH中,∵∠HBC=30°,∴BH=![]() CH=
CH=![]() ,∴AB=AH+BH=
,∴AB=AH+BH=![]() ≈141.4+244.9≈386.
≈141.4+244.9≈386.
答:两棵大树A和B之间的距离约为386米.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】在我县中学生春季田径运动会上,参加男子跳高的16名运动员的成绩如下表所示:
成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 1 | 3 | 3 | 4 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.1.70,1.65
B.1.70,1.70
C.1.65,1.70
D.3,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察一列数a1=3,a2=32,a3=33,a4=34,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是_______;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a6=_______,an=_______;(可用幂的形式表示)
(2)如果想要求l+2+22+23+...+210的值,可令S10=l+2+22+23+...+210①,将①式两边同乘以2,得_______②,由②减去①式,得S10=_______.
(3)若(1)中数列共有20项,设S20=3+32+33+34+…+320,请利用上述规律和方法计算S20的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中①∠DCF=![]() ∠BCD;②EF=CF;
∠BCD;②EF=CF;
③S△BEC=2S△CEF;④∠DFE=3∠AEF.一定成立的是( )

A. ①② B. ①③④ C. ①②③ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一家苗圃计划植桃树和柏树,根据市场调查与预测,种植桃树的利润![]() (万元)与投资成本x(万元)满足如图①所示的二次函数
(万元)与投资成本x(万元)满足如图①所示的二次函数![]() ;种植柏树的利润
;种植柏树的利润![]() (万元)与投资成本x(万元)满足如图②所示的正比例函数
(万元)与投资成本x(万元)满足如图②所示的正比例函数![]() =kx.
=kx.

(1)分别求出利润![]() (万元)和利润
(万元)和利润![]() (万元)关于投资成本x(万元)的函数关系式;
(万元)关于投资成本x(万元)的函数关系式;
(2)如果这家苗圃以10万元资金投入种植桃树和柏树,桃树的投资成本不低于2万元且不高于8万元,苗圃至少获得多少利润?最多能获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
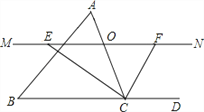
【题目】如图,在△ABC中,点O是边AC上一个动点(不与点A、C重合),过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)探究OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动到什么位置,四边形AECF是矩形,请说明理由;
(3)在第(2)问的基础上,△ABC满足什么条件时,四边形AECF是正方形?(不需说明理由)
(4)当点O在边AC上运动时,四边形BCFE能成为菱形吗?若能,请加以证明;若不能,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com