
 如图,甲船以每小时30$\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的南偏西方向30°的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向B2处,此时两船相距10$\sqrt{2}$海里,问乙船每小时航行多少海里?
如图,甲船以每小时30$\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的南偏西方向30°的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向B2处,此时两船相距10$\sqrt{2}$海里,问乙船每小时航行多少海里? 分析 连结A1B2,如图,先计算出A1A2=10$\sqrt{2}$(海里),再判断△A1A2B2为等边三角形得到A1B2=10$\sqrt{2}$,∠A2A1B2=60°,则可计算出∠B1A1B2=90°,然后利用勾股定理可计算出B1B2,再利用速度公式计算乙船航行的速度即可.
解答 解:连结A1B2,如图,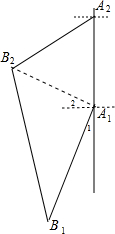 A1A2=30$\sqrt{2}$×$\frac{20}{60}$=10$\sqrt{2}$(海里)
A1A2=30$\sqrt{2}$×$\frac{20}{60}$=10$\sqrt{2}$(海里)
∵∠A1A2B2=60°,A1A2=A2B2=10$\sqrt{2}$,
∴△A1A2B2为等边三角形,
∴A1B2=10$\sqrt{2}$,∠A2A1B2=60°,
∵∠1=30°,
∴∠B1A1B2=180°-30°-60°=90°,
在Rt△B1A1B2中,B1B2=$\sqrt{{A}_{1}{{B}_{1}}^{2}+{A}_{1}{{B}_{2}}^{2}}$=$\sqrt{2{0}^{2}+(10\sqrt{2})^{2}}$=10$\sqrt{6}$,
∴乙船航行的速度=$\frac{10\sqrt{6}}{\frac{1}{3}}$=30$\sqrt{6}$(海里/时).
答:乙船每小时航行30$\sqrt{6}$海里.
点评 本题考查了解直角三角形的应用-方向角问题:在辨别方向角问题中,一般是以第一个方向为始边向另一个方向旋转相应度数.在解决有关方向角的问题中,一般要根据题意理清图形中各角的关系,有时所给的方向角并不一定在直角三角形中,需要用到两直线平行内错角相等或一个角的余角等知识转化为所需要的角.


科目:初中数学 来源: 题型:选择题
 如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )
如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )| A. | △ABD∽△ACE | B. | ∠B=∠C | C. | BD=2CE | D. | AB•EC=AC•BD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10),请你结合表格和图象:
某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10),请你结合表格和图象:| 付款金额 | a | 7.5 | 10 | 12 | b |
| 购买量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小强由甲地匀速步行到乙地后原路返回,小亮由甲地匀速步行经乙地到丙地后原路返回,两人同时出发,他们离乙地的路程S(km)与步行的时间t(h)间的函数关系如图所示,则下列说法中正确的个数有( )
小强由甲地匀速步行到乙地后原路返回,小亮由甲地匀速步行经乙地到丙地后原路返回,两人同时出发,他们离乙地的路程S(km)与步行的时间t(h)间的函数关系如图所示,则下列说法中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com