
 完成下面推理过程.在括号内的横线上填空或填上推理依据.
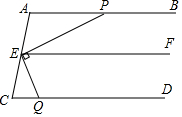
完成下面推理过程.在括号内的横线上填空或填上推理依据.分析 根据平行线的性质得到∠APE=∠PEF,根据余角的性质得到∠EQC=∠QEF根据平行线的判定定理即可得到结论.
解答 证明:∵AB∥EF
∴∠APE=∠PEF(两直线平行,内错角相等)
∵EP⊥EQ
∴∠PEQ=90°(垂直的定义)
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
∵∠EQC+∠APE=90°
∴∠EQC=∠QEF
∴EF∥CD(内错角相等,两直线平行)
∴AB∥CD(平行公理),
故答案为:∠PEF,两直线平行,内错角相等,90°,∠QEF,内错角相等,两直线平行,CD,平行公理.
点评 本题考查了平行线的判定和性质,垂直的定义,熟练掌握平行线的判定和性质是解题的关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
 -(a2b-2ab2)+ab2=2(a2b+ab2).试问,老师用手捂住的多项式是什么?
-(a2b-2ab2)+ab2=2(a2b+ab2).试问,老师用手捂住的多项式是什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
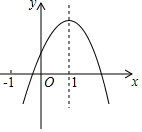 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,下列结论中正确的是( )| A. | ab>0 | B. | b=2a | C. | 4a+2b+c<0 | D. | a+c<b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com