
【题目】为满足同学们课外阅读的需求,某中学图书馆向出版社邮购科普系列图书,每本书单价为16元,书的价钱和邮费是通过邮局汇款,相关的书价折扣、邮费和汇款的汇费如下表所示(总费用=总书价+总邮费+总汇费)
购书数量 | 折扣 | 邮费 | 汇费 |
不超过10本 | 九折 | 6元 | 每100元汇款需汇费1元 (汇款不足100元时按100元汇款收汇费) |
超过10本 | 八折 | 总书价的10% | 每100元汇款需汇费1元 (汇款不足100元的部分不收汇费) |
(1)若一次邮购7本,共需总费用为 元.
(2)已知学校图书馆需购图书的总数是10的整倍数,且超过10本.
①若分次邮购,分别汇款,每次邮购10本,总费用为1064元时,共邮购了多本图书?
②若你是学校图书馆负责人,从节约的角度出发,在“每次邮购10本“与“一次性邮购”这两种方式中选择一种,你会选择哪一种?计算并说明理由.
【答案】(1)108.8元;(2)①共邮购了70本;②从节约的角度出发,选择一次性邮购的方式,理由见解析.
【解析】
(1)根据总费用=7本书的总价×0.9+总邮费+总汇费就可以求出结论;
(2)①设一共邮购了x本书,分![]() 邮购,需要书款为
邮购,需要书款为![]() 元,邮费为
元,邮费为![]()
元,汇费为![]() 元,根据题意建立方程求出其解就可以了;
元,根据题意建立方程求出其解就可以了;
②分别计算出每次邮购10本和一次邮购的总费用的表达式,再比较其大小就可以得出结论;
(1)由题意可得,
总书价为:16×7×0.9=100.8(元),
∴总的费用为:100.8+6+2=108.8(元),
故答案为:108.8元;
(2)①设共邮购了x本图书,
16×10×0.9=144(元),
∴![]()
解得,x=70,
答:共邮购了70本;
②从节约的角度出发,选择一次性邮购的方式,
理由:设共购买了x本,
按每次邮购10本,最后的总费用为:![]() (元),
(元),
一次性邮购的总书价和邮费为:16×0.8x(1+10%)=14.08x,
∵超过10本,不足100元的部分不收汇费,
∴汇费不大于:0.1408x元,
∵15.2x﹣(14.08x+0.1408x)=0.9792x>0,
∴从节约的角度出发,选择一次性邮购的方式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.
(1)求这个二次函数的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;
(3)设(2)中平移后所得二次函数图象与y轴的交点为B1 , 顶点为D1 . 点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,它们除颜色外都相同。
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率不小于![]() ,问至少取出了多少个黑球?
,问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点O是等边△ABC内的任一点,连接OA,OB,OC.
(1)如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①∠DAO的度数是多少?
②用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)设∠AOB=α,∠BOC=β.
①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;
②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2(x+1)(x﹣a),其中a>0,若当x≤2时,y随着x增大而减小,当x≥2时y随着x的增大而增大,则a的值是( )
A.3
B.5
C.7
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程:①3x﹣1=2x+1,②![]() ,③
,③![]() ,④
,④![]() x﹣1=x中,解为x=2的是方程( )
x﹣1=x中,解为x=2的是方程( )
A. ①、②和③ B. ①、③和④ C. ②、③和④ D. ①、②和④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,∠AOB=90°,OA=3,将扇形OAB绕点A逆时针旋转n°(0<n<180)后得到扇形O′AB′,当点O在弧AB′上时,n为 , 图中阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形纸片,剪下一个正方形,剩下一个长方形,称为第一次操作;在剩下的长方形纸片中再剪下一个正方形,剩下一个长方形,称为第二次操作;…;若在第n次操作后,剩下的长方形为正方形,则称原长方形为n阶奇异长方形.如图1,长方形ABCD中,若AB=2,BC=6,则称长方形ABCD为2阶奇异长方形.

(1)判断与操作:如图2,长方形ABCD长为10,宽为6,它是奇异长方形,请写出它是____阶奇异长方
形,并在图中画出裁剪线;
探究与计算:已知长方形ABCD的一边长为24,另一边长为a (a<24),且它是3阶奇异长方形,请画出所
有可能的长方形ABCD及裁剪线的示意图,并求出相应的a值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )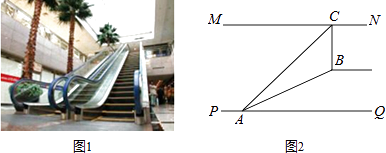
A.10.8米
B.8.9米
C.8.0米
D.5.8米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com