
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若AB=3,BC=4,求四边形OCED的面积.

【答案】(1)见解析;(2)6
【解析】试题分析:
(1) 观察题目中的两组平行线易知,四边形OCED的两组对边分别平行,即四边形OCED是平行四边形. 在平行四边形的基础上若想证明其为菱形,则要么再证一组邻边相等要么再证对角线互相垂直. 继续观察图形可知,利用矩形ABCD的性质证明OC与OD相等是容易的. 因此,根据一组邻边相等的平行四边形为菱形即可证明四边形OCED是菱形.
(2) 分析条件可知,在矩形ABCD中,AB=CD=3,线段CD恰好是菱形OCED的一条对角线,于是容易想到利用对角线乘积的一半去计算菱形的面积. 作出菱形的另一条对角线OE,利用菱形OCED的性质和矩形ABCD的性质可知OE∥BC,进而得到四边形OBCE为平行四边形,再利用平行四边形的性质可求得OE的长度. 在得到两条对角线的长度后,按菱形的面积公式即可得到四边形OCED的面积.
试题解析:
(1) 证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴OC= ![]() ,OD=
,OD= ![]() ,AC=BD,
,AC=BD,
∴OC=OD,
∴平行四边形OCED为菱形.
(2) 四边形OCED的面积为6. 求解过程如下.
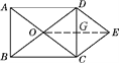
连接OE,交CD于点G. (如图)
∵四边形OCED为菱形,
∴OE⊥CD,
∴∠OGD=90°,
∵四边形ABCD为矩形,
∴∠BCD=90°,
∴∠OGD=∠BCD,
∴OE∥BC,
∵CE∥BD,OE∥BC,
∴四边形OBCE为平行四边形,
∴OE=BC,
∵四边形ABCD为矩形,
∴CD=AB,
∵AB=3,BC=4,
∴CD=AB=3,OE=BC =4,
∴菱形OCED的面积为![]() ,
,
即四边形OCED的面积为6.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c的顶点A在x轴上,与y轴的交点B(0,-1),且b=-4ac。
(1)求点A的坐标;
(2)求抛物线的解析式
(3)在抛物线上是否存在一点C,使以BC为直径的圆经过抛物线的顶点A?若不存在请说明理由;若存在,求出点C的坐标,并求出此时圆的圆心点P的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一间摄影展览厅,其东、西面各有一个入口A、B,南面为出口C,北面分别有两个出口D、E,摄影爱好者郑浩任选一个入口进入展览厅,参观结束后,任选一个出口离开。
(1)郑浩从进入到离开共有多少种可能的结果?请画出树形图;
(2)求出郑浩从入口A进入展览厅并从北面出口离开的概率。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家庭农场要建一个长方形的养兔场,兔场的两边靠墙(两堵墙互相垂直,长度不限),另两边用木栏围成,木栏总长20米.
(1)兔场的面积能达到100平方米吗?请你给出设计方案;
(2)兔场的面积能达到110平方米吗?如能,请给出设计方案,若不能说明理.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com