
【题目】在自习课上,小明拿来如下框的一道题目(原问题)和合作学习小组的同学们交流.
如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB,BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F.探究线段DF与EF的数量关系.
小红同学的思路是:过点D作DG⊥AB于点G,构造全等三角形,通过推理使问题得解.
小华同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.
请你参考小明同学的思路,探究并解决以下问题:
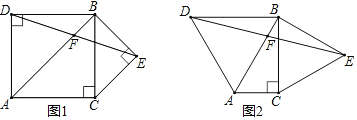
(1)写出原问题中DF与EF的数量关系为 .
(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.
【答案】(1)DF=EF;(2)不发生变化,理由见解析
【解析】
(1)结论:DF=EF.只要证明△DFG≌△EFB(AAS)即可解决问题;
(2)猜想:DF=FE.过点D作DG⊥AB于G,则∠DGB=90°.由Rt△DBG≌Rt△BAC(HL),推出DG=BC,再证明△DFG≌△EFB(AAS)即可解决问题;
解:(1)结论:DF=EF.
理由:作DG⊥AB于G.
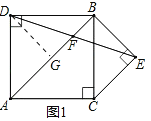
∵∠DBG=∠CBE=45°,∠DGB=∠BEC=90°,DB=BC,
∴△DBG≌△BCE(AAS),
∴GD=BE,
∵∠DGB=∠GBE=90°,
∴DG∥BE,
∴∠FDG=∠BEF,
∵∠DFG=∠BFE,
∴△DFG≌△EFB(AAS),
∴DF=EF.
故答案为DF=EF.
(2)猜想:DF=FE.
理由:过点D作DG⊥AB于G,则∠DGB=90°.
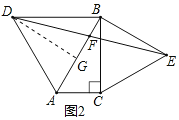
∵DA=DB,∠ADB=60°.
∴AG=BG,△DBA是等边三角形,
∴DB=BA,
∵∠ACB=90°,∠ABC=30°,
∴AC=![]() AB=BG,
AB=BG,
在Rt△DBG和Rt△BAC中,
![]()
∴Rt△DBG≌Rt△BAC(HL),
∴DG=BC,
∵BE=EC,∠BEC=60°,
∴△EBC是等边三角形,
∴BC=BE,∠CBE=60°,
∴DG=BE,∠ABE=∠ABC+∠CBE=90°,
在△DFG和△EFB中,
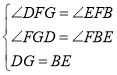
∴△DFG≌△EFB(AAS),
∴DF=EF.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
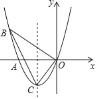
【题目】如图,已知抛物线y=ax2+bx经过点A(﹣2,0)、B(﹣3,3),顶点为C.
(1)求抛物线的函数表达式;
(2)若点P是第一象限内的抛物线上一动点,过点P作PM⊥x轴于点M,则是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左边到右边的变形,是因式分解的是( )
A.y![]() ﹣5y﹣6=(y﹣6)(y+1)B.a
﹣5y﹣6=(y﹣6)(y+1)B.a![]() +4a﹣3=a(a+4)﹣3
+4a﹣3=a(a+4)﹣3
C.x(x﹣1)=x![]() ﹣xD.m
﹣xD.m![]() +n
+n![]() =(m+n)(m﹣n)
=(m+n)(m﹣n)
查看答案和解析>>
科目:初中数学 来源: 题型:
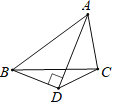
【题目】有些数学题,表面上看起来无从下手,但根据图形的特点,可补全成为特殊的图形,然后根据特殊几何图形的性质去考虑,常常可以获得简捷解法.根据阅读,请解答问题:如图所示,已知△ABC的面积为16cm2,AD平分∠BAC,且AD⊥BD于点D,则△ADC的面积为___________cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考
x2+(p+q)x+pq型式子的因式分解
x2+(p+q)x+pq型式子是数学学习中常见的一类多项式,如何将这种类型的式子分解因式呢?
我们通过学习,利用多项式的乘法法则可知:(x+p)(x+q)=x2+(p+q)x+pq,因式分解是整式乘法相反方向的变形,利用这种关系可得x2+(p+q)x+pq=(x+p)(x+q).
利用这个结果可以将某些二次项系数是1的二次三项式分解因式,例如,将x2﹣x﹣6分解因式.这个式子的二次项系数是1,常数项﹣6=2×(﹣3),一次项系数﹣1=2+(﹣3),因此这是一个x2+(p+q)x+pq型的式子.所以x2﹣x﹣6=(x+2)(x﹣3).
上述过程可用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数,如图所示.
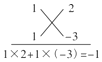
这样我们也可以得到x2﹣x﹣6=(x+2)(x﹣3).这种分解二次三项式的方法叫“十字相乘法”.
请同学们认真观察,分析理解后,解答下列问题:
(1)分解因式:y2﹣2y﹣24.
(2)若x2+mx﹣12(m为常数)可分解为两个一次因式的积,请直接写出整数m的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目.为了解学生最喜爱哪一种项目,童威随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出)
(1)本次被调查的学生人数为 ,扇形统计图中“跑步”所对的圆心角为 度.
(2)补全条形统计图;
(3)该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
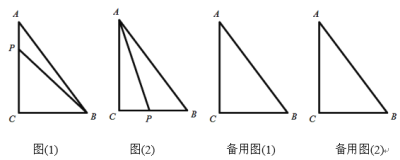
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点P从点A开始沿着
,若动点P从点A开始沿着![]() 的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
的路径运动,且速度为每秒2cm,设点P运动的时间为t秒.
(1)当![]() 时,
时,![]() 的面积是___________
的面积是___________![]() ;
;
(2)如图(2)当t为何值时,AP平分![]() ;
;
(3)当t为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com