
【题目】在直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,按如图方式作正方形
,按如图方式作正方形![]() 、
、![]() 、
、![]() ,点
,点![]() 、
、![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 、
、![]() 在
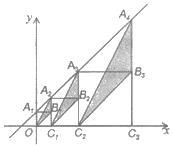
在![]() 轴上,图中阴影部分三角形的面积从左到右依次记为
轴上,图中阴影部分三角形的面积从左到右依次记为![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为__________.
的值为__________.
【答案】![]()
【解析】
结合正方形的性质结合直线的解析式可得出:A2B1=OC1,A3B2=C1C2,A4B3=C2C3,…,结合三角形的面积公式即可得出:S1=![]() OC12=,S2=C1C22=2,S3=
OC12=,S2=C1C22=2,S3=
![]() C2C32=8,…,根据面积的变化可找出变化规律“Sn=22n-3(n为正整数)”,依此规律即可得出结论.
C2C32=8,…,根据面积的变化可找出变化规律“Sn=22n-3(n为正整数)”,依此规律即可得出结论.
解:令一次函数y=x+1中x=0,则y=1,
∴点A1的坐标为(0,1),OA1=1.
∵四边形AnBnCnCn-1(n为正整数)均为正方形,
∴A1B1=OC1=1,A2B2=C1C2=2,A3B3=C2C3=4,….
令一次函数y=x+1中x=1,则y=2,
即A2C1=2,
∴A2B1=A2C1-A1B1=1=A1B1,
∴tan∠A2A1B1=1.
∵AnCn-1⊥x轴,
∴tan∠An+1AnBn=1.
∴A2B1=OC1,A3B2=C1C2,A4B3=C2C3,….
∴S1=![]() OC12=
OC12=![]() ,S2=C1C22=2,S3=
,S2=C1C22=2,S3=![]() C2C32=8,…,
C2C32=8,…,
∴Sn=22n-3(n为正整数),∴![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c(b,c是常数)的图象经过点(1,﹣1).
(1)用含b的代数式表示c.
(2)求二次函数图象的顶点纵坐标的最大值,并写出此时二次函数的表达式.
(3)垂直于y轴的直线与(2)中所得的二次函数图象交于(x1,y1)和(x2,y2),与一次函数y=﹣x+2的图象交于(x3,y3),若x1<x2<x3,求x1+x2+x3的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①abc<0;②4ac<b2;③方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;④3a+c>0;⑤当y≥0时,x的取值范围是﹣1≤x≤3.其中结论正确的个数是( )
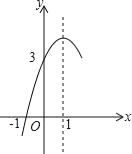
A. 1个B. 2个C. 3D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中B点坐标是(8,2),D点坐标是(0,2),点A在x轴上,则菱形ABCD的周长是( )
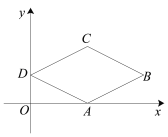
A.2![]()
B.8
C.8![]()
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中给出![]() ,
,![]() ,
,![]() 三种手机通话的收费方式.
三种手机通话的收费方式.
收费方式 | 月通话费/元 | 包时通话时间/ | 超时费/(元/ |
|
|
|
|
|
|
|
|
|
| 不限时 |
(1)设月通话时间为![]() 小时,则方案
小时,则方案![]() ,
,![]() ,
,![]() 的收费金额
的收费金额![]() ,
,![]() ,
,![]() 都是
都是![]() 的函数,请分别求出这三个函数解析式.
的函数,请分别求出这三个函数解析式.
(2)填空:
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
(3)小王、小张今年![]() 月份通话费均为
月份通话费均为![]() 元,但小王比小张通话时间长,求小王该月的通话时间.
元,但小王比小张通话时间长,求小王该月的通话时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
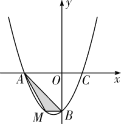
【题目】(2010河南23题)在平面直角坐标系中,已知抛物线经过![]() ,
,![]() ,
,![]() 三点.
三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,![]() 的面积为S.求S关于m的函数关系式,并求出S的最大值;
的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的距离CD=2.8米,一楼到地平线的距离BC=1米.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?(结果精确到0.1米)
(2)如果给该商场送货的货车高度为2.5米,那么按这样的设计能否保证货车顺利进入地下停车场?请说明理由.(参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)

查看答案和解析>>
科目:初中数学 来源: 题型:
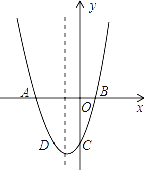
【题目】(12分)已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB,CD边于点E,F.
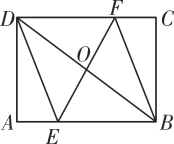
(1)求证:四边形DEBF是平行四边形;
(2)当DE=DF时,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com