
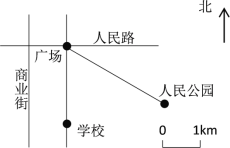
【题目】下面是某街区的平面示意图,根据要求答题.

(1)这幅图的比例尺是( )
(2)学校位于广场的( )面(填东、南、西、北)( )千米处.
(3)人民公园位于广场的东偏南![]() 方向3千米处.在图中标出它的位置.
方向3千米处.在图中标出它的位置.
(4)广场的西面1千米处,有一条商业街与人民路垂直,在图中画线表示商业街.
【答案】(1)1:100000;(2)南;2;(3)图见解析;(4)图见解析
【解析】
(1)由线段比例可知,图上1cm表示实际距离1km,根据比例尺公式即可求出结论;
(2)测量出学校到广场的图上距离,根据比例尺公式即可求出实际距离,从而得出结论;
(3)先求出人民公园与广场的图上距离,然后根据方位角和距离画图即可;
(4)先求出商业街与广场的图上距离,然后画图即可.
解:(1)由图可知:这幅图的比例尺是1cm:1km=1:100000
故答案为:1:100000;
(2)由图可知:学校位于广场的南面,测量可知:学校到广场的图上距离为2cm
∴学校到广场的实际距离为2÷![]() =200000cm=2km
=200000cm=2km
故答案为:南;2;
(3)3千米=300000厘米
∴人民公园位于广场的东偏南![]() 方向,图上距离为300000×
方向,图上距离为300000×![]() =3厘米
=3厘米
如下图所示,人民广场即为所求;
(4)1千米=100000厘米
∴商业街与广场的图上距离为100000×![]() =1厘米
=1厘米
如上图所示,商业街即为所求.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图,点P在正方形ABCD边AD上,连接PB,过点B作一条射线与边DC的延长线交于点 Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ,若PQ=PB+PD+3,则△PAB的面积为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加“仙桃市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(l)班 86,85,77,92,85;八(2)班 79,85,92,85,89.通过数据分析,列表如下:
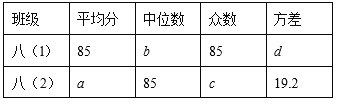
(1)直接写出表中a,b,c,d的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图象解一元二次方程x2-2x-1=0时,我们采用的一种方法是在直角坐标系中画出抛物线y=x2和直线y=2x+1,两图象交点的横坐标就是该方程的解.
(1)请再给出一种利用图象求方程x2-2x-1=0的解的方法;
(2)已知函数y=x3的图象(如图),求方程x3-x-2=0的解(结果保留两位有效数字).
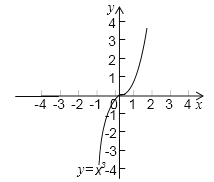
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于A,B两点,其顶点P在折线C-D-E上移动,若点C,D,E的坐标分别为(-1,4),(3,4),(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() (
(![]() 为正整数)都在数轴上,点
为正整数)都在数轴上,点![]() 在原点
在原点![]() 的左边,且
的左边,且![]() ;点
;点![]() 在点
在点![]() 的右边,且
的右边,且![]() ;点
;点![]() 在点
在点![]() 的左边,且
的左边,且![]() ;点
;点![]() 在点
在点![]() 的右边,且
的右边,且![]() ;…,依照上述规律,点
;…,依照上述规律,点![]() 所表示的数分别为 ( )
所表示的数分别为 ( )
A.2018,-2019B.1009,-1010C.-2018,2019D.-1009,1009
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于F,连接EF,若AB=4,若BC=6,则DF的长为_______ .
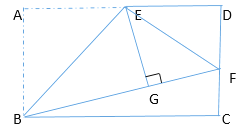
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC中点,过点D的直线GF交AC于F,交AC的平行线BG于G,DE⊥DF,交AB于E,连接BG,请你判断BE+CF与EF的大小关系,请说明理由.
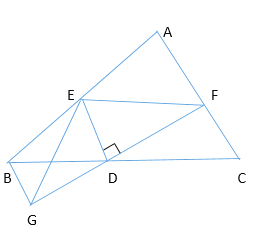
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O在直线AB上,点A1、A2、A3,…在射线OA上,点B1、B2、B3,…在射线OB上,图中的每一个实线段和虚线段的长均为一个单位长度,一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度,按此规律,则动点M到达A101点处所需时间为____秒.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com