Question

6．如图1，将两根笔直细木板MN、EF用图钉固定并平行摆放，将一根橡皮筋拉直后用图钉分别固定在MN、EF上，橡皮筋的两端点分别记为点A、点B．
（1）图1中，若∠1=110°，则∠2=70度．（直接写出结果，不需说理）
（2）P为橡皮筋上一点，利用橡皮筋的弹性拉动橡皮筋，使A、P、B三点不在同一直线上，然后用图钉固定点P．
①如图2，若点P在两细木棒所在直线之间，且∠1+∠2=90°，试判断线段AP与BP所在直线的位置关系，并说明理由；
②如图3，若点P在两细木棒所在直线的同侧，且∠1+∠2=90°，∠APB=28°，试求∠1、∠2的度数．
（3）P₁、P₂为AB上两点，拉动橡皮筋并固定如图4，若∠1+∠2=90°，则∠AP₁P₂+∠BP₂P₁=270度．（直接写出结果，不需说理）

Answer 1

分析 （1）根据MN∥EF即可得出∠1+∠2=180°，结合∠1=110°即可求出∠2的度数；
（2）①过点P作PC∥MN，根据MN∥EF即可得出PC∥MN∥EF，进而得出∠APC=∠1，∠BPC=∠2，再根据角与角之间的关系即可得出∠APB=∠1+∠2=90°，由此即可得出AP⊥BP；
②过点P作PD∥MN，同理可得出∠APC=∠1，∠BPC=∠2，根据角与角之间的关系即可得出∠APB=∠2-∠1=28°，再结合∠1+∠2=90°，即可求出∠1、∠2的度数；
（3）过点P₁作P₁C∥MN，过点P₂作P₂D∥MN，由MN∥EF即可得出P₁C∥MN∥EF∥P₂D，从而可得出∠1=∠AP₁C，∠2=∠BP₂D，∠CP₁P₂+∠DP₂P₁=180°，再根据角与角之间的关系即可算出∠AP₁P₂+∠BP₂P₁的度数．

解答 解：（1）∵MN∥EF，
∴∠1+∠2=180°，
∵∠1=110°，
∴∠2=70°．
故答案为：70．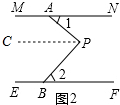
（2）①AP⊥BP，理由如下：
在图2中，过点P作PC∥MN，
∵MN∥EF，
∴PC∥MN∥EF，
∴∠APC=∠1，∠BPC=∠2．
∵∠APB=∠APC+∠BPC，∠1+∠2=90°，
∴∠APB=90°，
∴AP⊥BP．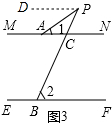
②在图3中，过点P作PD∥MN，
∵MN∥EF，
∴PD∥MN∥EF，
∴∠DPA=∠1，∠DPB=∠2，
∴∠APB=∠DPB-∠DPA=∠2-∠1=28°．
又∵∠1+∠2=90°，
∴∠1=31°，∠2=59°．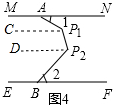
（3）在图4中，过点P₁作P₁C∥MN，过点P₂作P₂D∥MN，
∵MN∥EF，
∴P₁C∥MN∥EF∥P₂D，
∴∠1=∠AP₁C，∠2=∠BP₂D，∠CP₁P₂+∠DP₂P₁=180°．
又∵∠1+∠2=90°，
∴∠AP₁P₂+∠BP₂P₁=∠AP₁C+∠CP₁P₂+∠BP₂D+∠DP₂P₁=（∠AP₁C+∠BP₂D）+（∠CP₁P₂+∠DP₂P₁）=90°+180°=270°．
故答案为：270．

点评 本题考查了平行线的性质，解题的关键是：（1）找出∠1+∠2=180°；（2）①求出∠APB=∠1+∠2=90°；②找出∠APB=∠2-∠1=28°；（3）根据平行线的性质找出∠1=∠AP₁C，∠2=∠BP₂D，∠CP₁P₂+∠DP₂P₁=180°．本题属于中档题，难度不大，解决该题型题目时，根据平行线的性质找出相等（或）互补的角是关键．