
在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,(如图)则∠EAF等于( )
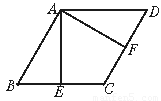
A.75° B.60° C.45° D.30°
B
【解析】
试题分析:首先连接AC,由四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,易得△ABC与△ACD是等边三角形,即可求得∠B=∠D=60°,继而求得∠BAD,∠BAE,∠DAF的度数,则可求得∠EAF的度数.
连接AC,
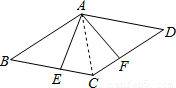
∵AE⊥BC,AF⊥CD,且E、F分别为BC、CD的中点,
∴AB=AC,AD=AC,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∴AB=BC=AC,AC=CD=AD,
∴∠B=∠D=60°,
∴∠BAE=∠DAF=30°,∠BAD=180°-∠B=120°,
∴∠EAF=∠BAD-∠BAE-∠DAF=60°.
故选C.
考点:此题考查了菱形的性质,线段垂直平分线的性质以及等边三角形的判定与性质
点评:解答本题的关键是熟练掌握菱形的性质,注意掌握辅助线的作法,注意数形结合思想的应用.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
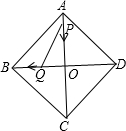 如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍.
如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com