
分析 (1)直接根据根与系数的关系求解;
(2)利用m、n满足的等式,可把m、n可看作方程2x2-2x-1=0的两实数解,则根据根与系数的关系得到m+n=1,mn=-$\frac{1}{2}$,接着把m2n+mn2分解得到mn(m+n),然后利用整体代入的方法计算;
(3)先设t=2q,代入2q2=3q+1化简得到t2=3t+2,根据p与t满足的等式可把p与t(即2q)为方程x2-3x-2=0的两实数解,则根据根与系数的关系得到p+2q=3,p•2q=-2,接着利用完全平方公式变形得到p2+4q2=(p+2q)2-2p•2q,然后利用整体代入的方法计算.
解答 解:(1)x1+x2=-$\frac{3}{2}$,x1x2=-$\frac{1}{2}$;
故答案为-$\frac{3}{2}$,-$\frac{1}{2}$;
(2)∵m、n满足2m2-2m-1=0,2n2-2n-1=0,
∴m、n可看作方程2x2-2x-1=0的两实数解,
∴m+n=1,mn=-$\frac{1}{2}$,
∴m2n+mn2=mn(m+n)=-$\frac{1}{2}$×1=-$\frac{1}{2}$;
(3)设t=2q,代入2q2=3q+1化简为t2=3t+2,
则p与t(即2q)为方程x2-3x-2=0的两实数解,
∴p+2q=3,p•2q=-2,
∴p2+4q2=(p+2q)2-2p•2q=32-2×(-2)=13.
点评 本题考查了根与系数的关系:二次项系数不为1,则常用以下关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


科目:初中数学 来源: 题型:解答题
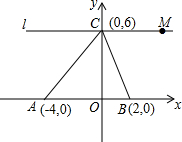 如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)
如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.134×102人 | B. | 613.4×104人 | C. | 6.134×105人 | D. | 6.134×106人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
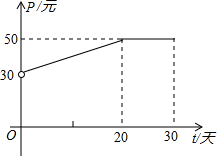 根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
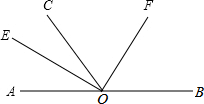 如图,AOB是一条直线,OC是一条射线,∠AOC=60°,OE、OF分别是∠AOC、∠BOC平分线.
如图,AOB是一条直线,OC是一条射线,∠AOC=60°,OE、OF分别是∠AOC、∠BOC平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com