
【题目】已知:![]() 是经过点A的一条直线,点C是直线
是经过点A的一条直线,点C是直线![]() 左侧的一个动点,且满足
左侧的一个动点,且满足![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点C顺时针旋转60°,得到线段
绕点C顺时针旋转60°,得到线段![]() ,在直线
,在直线![]() 上取一点B,使
上取一点B,使![]() .
.
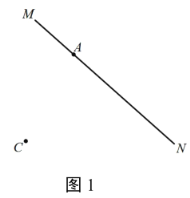
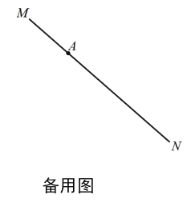
(1)若点C位置如图1所示.
①依据题意补全图1;
②求证:![]() ;
;
(2)连接![]() ,写出一个
,写出一个![]() 的值,使得对于任意一点C,总有
的值,使得对于任意一点C,总有![]() ,并证明.
,并证明.
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴是![]() ,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
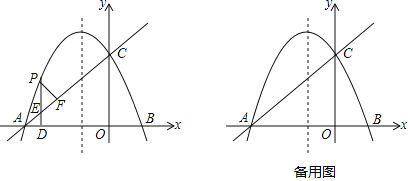
(1)求抛物线和直线l的解析式;
(2)点P是直线AC上方的抛物线上一个动点,过点P作PD⊥x轴于点D,交AC于点E,过点P作PF⊥AC,垂足为F,当△PEF≌△AED时,求出点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,直接写出所有满足条件的Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把![]() 个只有颜色不同的小球分别装入甲乙丙三个布袋里其中甲布袋里有
个只有颜色不同的小球分别装入甲乙丙三个布袋里其中甲布袋里有![]() 个红球,
个红球,![]() 个白球;乙布袋里有
个白球;乙布袋里有![]() 个红球,
个红球,![]() 个白球;丙布袋里有
个白球;丙布袋里有![]() 个红球,
个红球,![]() 个白球.
个白球.
![]() 求
求![]() 的值,并求从甲、乙两个布袋中随机各摸出
的值,并求从甲、乙两个布袋中随机各摸出![]() 个小球,求摸出的两个小球都是红球的概率;
个小球,求摸出的两个小球都是红球的概率;
![]() 利用列表或树状图法求从甲、乙、丙三个布袋中随机各摸出
利用列表或树状图法求从甲、乙、丙三个布袋中随机各摸出![]() 个小球,求摸出的三个小球是一红二白的概率.
个小球,求摸出的三个小球是一红二白的概率.
![]() 将丙袋子中原有的所有小球拿出,另装
将丙袋子中原有的所有小球拿出,另装![]() 个只有颜色不同的球,其中
个只有颜色不同的球,其中![]() 个白球,
个白球,![]() 个红球,若从袋中取出若千个红球,换成相同数量的黄球.搅拌均匀后,使得随机从袋中摸出两个球,颜色是一白一黄的概率为
个红球,若从袋中取出若千个红球,换成相同数量的黄球.搅拌均匀后,使得随机从袋中摸出两个球,颜色是一白一黄的概率为![]() ,(不放回拿球)求袋中有几个红球被换成了黄球?
,(不放回拿球)求袋中有几个红球被换成了黄球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)当k取满足(1)中条件的最小整数时,设方程的两根为α和β,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办初中生数学素养大赛,比赛共设四个项目:七巧拼图、趣题巧解、数学应用和魔方复原,每个项目得分都按一定百分比折算后记入总分,并规定总分在85分以上(含85分)设为一等奖.下表为甲、乙、丙三位同学的得分情况(单位:分),其中甲的部分信息不小心被涂黑了.
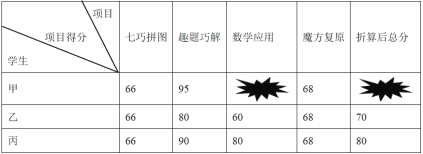
据悉,甲、乙、丙三位同学的七巧拼图和魔方复原两项得分折算后的分数之和均为20分.设趣题巧解和数学应用两个项目的折算百分比分别为x和y,请用含x和y的二元一次方程表示乙同学“趣题巧解和数学应用”两项得分折算后的分数之和为_________________;如果甲获得了大赛一等奖,那么甲的“数学应用”项目至少获得_________分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是正方形ABCD的对角线AC上的两点,AE=CF,连接DE、BE、BF、DF.
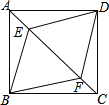
(1)求证:四边形BEDF为菱形;
(2)若菱形BEDF的边长为2![]() ,AE=2,求正方形ABCD的边长.
,AE=2,求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如图所示的函数图象是由函数y=(x﹣1)2+1(x≥0)的图象C1和图象C2组成中心对称图形,对称中心为点(0,2).已知不重合的两点A、B分别在图象C1和C2上,点A、B的横坐标分别为a、b,且a+b=0.当b<x≤a时该函数的最大值和最小值均与a、b的值无关,则a的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点M在直线![]() 外,点N在直线
外,点N在直线![]() 上,请用无刻度的直尺和圆规完成下列作图,要求保留痕迹,不写作法.
上,请用无刻度的直尺和圆规完成下列作图,要求保留痕迹,不写作法.
(1)在图①中,以线段MN为一条对角线作菱形MPNQ,使菱形的边PN落在直线![]() 上
上
(2)在图②中,做圆O,使圆O过点M,且与直线![]() 相切于N.
相切于N.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com